题目内容
(1)设集合A={x|x2-2x-3<0},B={x|x-a>0},若A∩B=A,求a的范围;
(2)设集合M={x∈R|ax2-3x-1=0},若集合M中至多有一个元素,求a的范围.
(2)设集合M={x∈R|ax2-3x-1=0},若集合M中至多有一个元素,求a的范围.
考点:交集及其运算,元素与集合关系的判断
专题:集合
分析:(1)分别求解二次不等式和一次不等式化简集合A,B,然后结合A∩B=A求得a的范围;
(2)分a=0和a≠0讨论,当a≠0时,由△≤0求解a的取值范围.
(2)分a=0和a≠0讨论,当a≠0时,由△≤0求解a的取值范围.
解答:
解:(1)A={x|x2-2x-3<0}={x|-1<x<3},B={x|x>a}
∵A∩B=A,故A⊆B,
∴a≤-1;
(2)当a=0时显然符合题意.
当a≠0时,由题意,△≤0,即9+4a≤0,解得a≤-
.
综上,a∈(-∞,-
]∪{0}
∵A∩B=A,故A⊆B,
∴a≤-1;
(2)当a=0时显然符合题意.
当a≠0时,由题意,△≤0,即9+4a≤0,解得a≤-
| 9 |
| 4 |
综上,a∈(-∞,-
| 9 |
| 4 |
点评:本题考查了交集及其运算,考查了集合关系的运用,体现了数学转化思想方法,是基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
图中,可表示函数y=f(x)的图象的只可能是( )
A、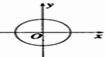 |
B、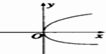 |
C、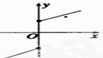 |
D、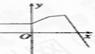 |
直线l:2x-2y+1=0的倾斜角为( )
| A、30° | B、45° |
| C、60° | D、90° |
若f(x)=x2-2(a-1)x+2在(-∞,3]上是减函数,则a的取值范围是( )
| A、a>4 | B、a<4 |
| C、a≥4 | D、a≤4 |