题目内容
已知三角形ABC的三个顶点的坐标为A(5,1),B(7,-3),C(2,-8),求直线AB及AB边上的中线的直线方程.
考点:直线的一般式方程
专题:直线与圆
分析:由中点坐标公式可得AB的中点D的坐标,由两点式可得直线的方程,化为一般式即可.
解答:
解:∵A(5,1),B(7,-3),C(2,-8),
∴AB的中点D(6,-1),
∴直线AB的方程为
=
,
化为一般式可得2x+y-11=0
同理可得AB边上的中线CD的方程为
=
.
化为一般式可得7x-4y-46=0
∴AB的中点D(6,-1),
∴直线AB的方程为
| y-1 |
| -3-1 |
| x-5 |
| 7-5 |
化为一般式可得2x+y-11=0
同理可得AB边上的中线CD的方程为
| y+8 |
| -1+8 |
| x-2 |
| 6-2 |
化为一般式可得7x-4y-46=0
点评:本题考查直线的一般式方程和中点坐标公式,属基础题.

练习册系列答案
相关题目
给出如下性质:①最小正周期为π;②图象关于直线x=
对称;③在(-
,
)上是增函数.则同时具有上述性质的一个函数是( )
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
A、y=sin(
| ||||
B、y=cos(
| ||||
C、y=sin(2x-
| ||||
D、y=cos(2x+
|
不等式(x+1)(3-x)<0的解集是( )
| A、(-1,3) |
| B、(-∞,-1)∪(3,+∞) |
| C、(-3,1) |
| D、(-∞,-3)∪(1,+∞) |
图中,可表示函数y=f(x)的图象的只可能是( )
A、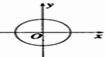 |
B、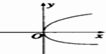 |
C、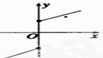 |
D、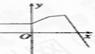 |
已知
=1-yi,其中x,y是实数,i是虚数单位,则复数x+yi的共轭复数对应的点位于为( )
| x |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
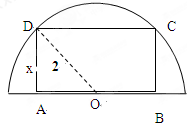 如图,有一块半径为2的半圆形钢板,计划剪裁成矩形ABCD的形状,设AD=x,矩形ABCD的面积为y,
如图,有一块半径为2的半圆形钢板,计划剪裁成矩形ABCD的形状,设AD=x,矩形ABCD的面积为y,