题目内容
设f(x)是定义在R上的奇函数,当x≤0时,f(x)=2x2-x,则f(2)=( )
| A、6 | B、-6 | C、10 | D、-10 |
考点:函数奇偶性的性质,函数的值
专题:函数的性质及应用
分析:运用奇偶性f(2)=-f(-2),代入求解即可.
解答:
解:∵f(x)是定义在R上的奇函数,
∴f(-x)=-f(x),
∵当x≤0时,f(x)=2x2-x,
∴f(2)=-f(-2)=-[2×(-2)2-(-2)]=-10,
故选:D
∴f(-x)=-f(x),
∵当x≤0时,f(x)=2x2-x,
∴f(2)=-f(-2)=-[2×(-2)2-(-2)]=-10,
故选:D
点评:本题考查了函数的性质,属于容易题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式(x+1)(3-x)<0的解集是( )
| A、(-1,3) |
| B、(-∞,-1)∪(3,+∞) |
| C、(-3,1) |
| D、(-∞,-3)∪(1,+∞) |
图中,可表示函数y=f(x)的图象的只可能是( )
A、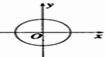 |
B、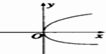 |
C、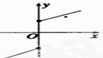 |
D、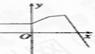 |
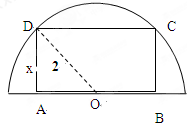 如图,有一块半径为2的半圆形钢板,计划剪裁成矩形ABCD的形状,设AD=x,矩形ABCD的面积为y,
如图,有一块半径为2的半圆形钢板,计划剪裁成矩形ABCD的形状,设AD=x,矩形ABCD的面积为y,