题目内容
1.一袋中装有5个白球,3个红球,现从袋中往外取球,每次任取一个,取出后记下颜色,若为红色停止,若为白色则继续抽取,停止时袋中抽取的白球的个数为随机变量ξ,则$P(ξ≤\sqrt{6})$=( )| A. | $\frac{9}{14}$ | B. | $\frac{25}{56}$ | C. | $\frac{37}{56}$ | D. | $\frac{23}{28}$ |
分析 ξ=k表示前k个为白球,第k+1个恰为红球,P(ξ≤$\sqrt{6}$)=P(ξ=0)+P(ξ=1)+P(ξ=2),由此能求出结果.
解答 解:ξ=k表示前k个为白球,第k+1个恰为红球,
P(ξ=0)=$\frac{{A}_{3}^{1}}{{A}_{8}^{1}}$=$\frac{3}{8}$,
P(ξ=1)=$\frac{{A}_{8}^{1}{A}_{3}^{1}}{{A}_{8}^{2}}$=$\frac{15}{56}$,
P(ξ=2)=$\frac{{A}_{8}^{2}{A}_{3}^{1}}{{A}_{8}^{3}}$=$\frac{10}{56}$,
P(ξ=3)=$\frac{{A}_{8}^{3}{A}_{3}^{1}}{{A}_{8}^{4}}$=$\frac{6}{56}$,
P(ξ=4)=$\frac{{A}_{8}^{4}{A}_{3}^{1}}{{A}_{8}^{5}}$=$\frac{3}{56}$,
P(ξ=5)=$\frac{{A}_{8}^{5}{A}_{3}^{1}}{{A}_{8}^{6}}$=$\frac{1}{56}$,
∴P(ξ≤$\sqrt{6}$)=P(ξ=0)+P(ξ=1)+P(ξ=2)
=$\frac{3}{8}+\frac{15}{56}+\frac{10}{56}$=$\frac{23}{28}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
11.某市5年中的煤气消耗量与使用煤气户数的历史资料如下:
(1)检验是否线性相关;
(2)求回归方程;
(3)若市政府下一步再扩大两千煤气用户,试预测该市煤气消耗量将达到多少?
| 年份 | 2006 | 2007 | 2008 | 2009 | 2010 |
| x用户(万户) | 1 | 1.1 | 1.5 | 1.6 | 1.8 |
| y(万立方米) | 6 | 7 | 9 | 11 | 12 |
(2)求回归方程;
(3)若市政府下一步再扩大两千煤气用户,试预测该市煤气消耗量将达到多少?
9.积分$\int_1^e{(\frac{1}{x}+2x)dx}$的值为( )
| A. | 1 | B. | e | C. | e+1 | D. | e2 |
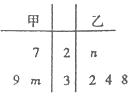 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同.