题目内容
9.积分$\int_1^e{(\frac{1}{x}+2x)dx}$的值为( )| A. | 1 | B. | e | C. | e+1 | D. | e2 |
分析 找出被积函数的原函数,计算定积分.
解答 解:原式=$(lnx+{x}^{2}){|}_{1}^{e}$=lne-ln1+e2-1=e2;
故选D.
点评 本题考查了定积分的计算;关键是正确找出原函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.抛物线x2=ay上有一点A(x0,2),它到焦点的距离是3,则其标准方程是( )
| A. | x2=y | B. | x2=2y | C. | x2=3y | D. | x2=4y |
14.某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差xi与实验室每天每100颗种子浸泡后的发芽数yi(i=1,2,…,5),作了初步处理,得到下表:
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于26”的概率;
(2)请根据3月1日至3月5日的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并预报3月份昼夜温差为14度时实验室每天100颗种子浸泡后的发芽(取整数值).
附:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的斜率和截距最小二乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,$\sum_{i=1}^5{{x_i}{y_i}=1351}$,$\sum_{i=1}^5{x_i^2}$=615.
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 温差xi(0C) | 10 | 11 | 13 | 12 | 9 |
| 发芽率yi(颗) | 23 | 25 | 30 | 26 | 16 |
(2)请根据3月1日至3月5日的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并预报3月份昼夜温差为14度时实验室每天100颗种子浸泡后的发芽(取整数值).
附:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的斜率和截距最小二乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,$\sum_{i=1}^5{{x_i}{y_i}=1351}$,$\sum_{i=1}^5{x_i^2}$=615.
1.一袋中装有5个白球,3个红球,现从袋中往外取球,每次任取一个,取出后记下颜色,若为红色停止,若为白色则继续抽取,停止时袋中抽取的白球的个数为随机变量ξ,则$P(ξ≤\sqrt{6})$=( )
| A. | $\frac{9}{14}$ | B. | $\frac{25}{56}$ | C. | $\frac{37}{56}$ | D. | $\frac{23}{28}$ |
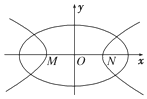 如图,中心均为原点O的椭圆与双曲线有公共焦点,M,N是双曲线的两顶点.若M,O,N将椭圆长轴四等分,则椭圆与双曲线的离心率的比值是为$\frac{1}{2}$.
如图,中心均为原点O的椭圆与双曲线有公共焦点,M,N是双曲线的两顶点.若M,O,N将椭圆长轴四等分,则椭圆与双曲线的离心率的比值是为$\frac{1}{2}$.