题目内容
13．
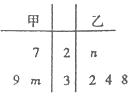已知甲、乙两组数据如茎叶图所示，若它们的中位数相同，平均数也相同．（1）求m，n的值；
（2）通过定量计算，试比较甲、乙两组数据的分散程度．
分析 （1）根据两组数据的中位数相同，平均数也相同，
求出m、n的值；
（2）计算平均数与方差，比较即可得出结论．
解答 解：（1）甲、乙两组数据如图茎叶图所示，
∵它们的中位数相同，平均数也相同，
∴30+m=$\frac{32+34}{2}$①，
$\frac{1}{3}$×（27+30+m+39）=$\frac{1}{4}$×（20+n+32+34+38）②，
由①②解得m=3，n=8；
（2）计算$\overline{{x}_{甲}}$=$\frac{1}{3}$（27+33+39）=33，
${{S}_{甲}}^{2}$=$\frac{1}{3}$[（27-33）2+（33-33）2+（39-33）2]=24，
$\overline{{x}_{乙}}$=$\overline{{x}_{甲}}$=33，
${{s}_{乙}}^{2}$=$\frac{1}{4}$[（28-33）2+（32-33）2+（34-33）2+（38-33）2]=13；
${{s}_{甲}}^{2}$＞${{s}_{乙}}^{2}$，所以乙组数据的稳定性更强．
点评 本题考查了利用茎叶图求平均数、方差的应用问题，是基础题．
练习册系列答案
习题精选系列答案
相关题目
某教育主管部门到一所中学检查学生的体质健康情况．从全体学生中，随机抽取12名进行体质健康测试，测试成绩（百分制）以茎叶图形式表示如下：根据学生体质健康标准，成绩不低于76的为优良．
1．一袋中装有5个白球，3个红球，现从袋中往外取球，每次任取一个，取出后记下颜色，若为红色停止，若为白色则继续抽取，停止时袋中抽取的白球的个数为随机变量ξ，则$P（ξ≤\sqrt{6}）$=（ ）
| A． | $\frac{9}{14}$ | B． | $\frac{25}{56}$ | C． | $\frac{37}{56}$ | D． | $\frac{23}{28}$ |
5．已知f（x）=2x-2-x，a=（$\frac{7}{9}$）${\;}^{-\frac{1}{4}}$，b=（$\frac{9}{7}$）${\;}^{\frac{1}{5}}$，c=log2$\frac{7}{9}$，则f（a），f（b），f（c）的大小顺序为（ ）
| A． | f（b）＜f（a）＜f（c） | B． | f（c）＜f（b）＜f（a） | C． | f（c）＜f（a）＜f（b） | D． | f（b）＜f（c）＜f（a） |
2．复数z=1+3i的模等于（ ）
| A． | 2 | B． | 4 | C． | $\sqrt{10}$ | D． | $2\sqrt{2}$ |