题目内容
12.设函数f(x)=ax3+bx+c(a>0)为奇函数,其图象在点(1,f(1))处的线与直线x-6y-7=0垂直,导函数f′(x)的最小值为-12.(1)求a,b,c的值;
(2)求函数f(x)的单调递增区间,并求函数f(x)在[-1,3]上的最大值和最小值.
分析 (1)先根据奇函数求出c的值,再根据导函数f'(x)的最小值求出b的值,最后依据在x=1处的导数等于切线的斜率求出c的值即可;
(2)先求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,求得区间即为单调区间,根据极值与最值的求解方法,将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,最小的一个就是最小值.
解答 解:(1)∵f(x)为奇函数,
∴f(-x)=-f(x),
即-ax3-bx+c=-ax3-bx-c,
∴c=0,
∵f'(x)=3ax2+b的最小值为-12,
∴b=-12,
又直线x-6y-7=0的斜率为$\frac{1}{6}$,
因此,f'(1)=3a+b=-6,
∴a=2,b=-12,c=0.
(2)f(x)=2x3-12x.f′(x)=6x2-12=6(x+$\sqrt{2}$)(x-$\sqrt{2}$),
列表如下:
| x | (-∞,-$\sqrt{2}$) | -$\sqrt{2}$ | (-$\sqrt{2}$,$\sqrt{2}$) | $\sqrt{2}$ | ($\sqrt{2}$,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大 | 递减 | 极小 | 递增 |
∵f(-1)=10,f($\sqrt{2}$)=-8$\sqrt{2}$,f(3)=18,
∴f(x)在[-1,3]上的最大值是f(3)=18,最小值是f($\sqrt{2}$)=-8$\sqrt{2}$.
点评 本题考查函数的奇偶性、单调性、二次函数的最值、导数的应用等基础知识,以及推理能力和运算能力.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
7.将参数方程$\left\{\begin{array}{l}x=2+sin2θ\\ y=sin2θ\end{array}$(θ为参数)化为普通方程是( )
| A. | y=x-2 | B. | y=x+2 | C. | y=x-2(1≤x≤3) | D. | y=x+2(0≤y≤1) |
1.一袋中装有5个白球,3个红球,现从袋中往外取球,每次任取一个,取出后记下颜色,若为红色停止,若为白色则继续抽取,停止时袋中抽取的白球的个数为随机变量ξ,则$P(ξ≤\sqrt{6})$=( )
| A. | $\frac{9}{14}$ | B. | $\frac{25}{56}$ | C. | $\frac{37}{56}$ | D. | $\frac{23}{28}$ |
2.复数z=1+3i的模等于( )
| A. | 2 | B. | 4 | C. | $\sqrt{10}$ | D. | $2\sqrt{2}$ |
 某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如下:根据学生体质健康标准,成绩不低于76的为优良.
某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如下:根据学生体质健康标准,成绩不低于76的为优良.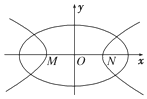 如图,中心均为原点O的椭圆与双曲线有公共焦点,M,N是双曲线的两顶点.若M,O,N将椭圆长轴四等分,则椭圆与双曲线的离心率的比值是为$\frac{1}{2}$.
如图,中心均为原点O的椭圆与双曲线有公共焦点,M,N是双曲线的两顶点.若M,O,N将椭圆长轴四等分,则椭圆与双曲线的离心率的比值是为$\frac{1}{2}$.