题目内容
已知函数f(x)=
,若f[f(x0)]=0,则x0= .
|
考点:分段函数的应用,函数的值
专题:函数的性质及应用
分析:当x∈(-∞,0)时f(x)=x2>0,若f[f(x0)]=0,则f(x0)的函数值为0,不可能,从而f(x0)∈(0,π)
易推f[f(x0)]=0中f(x0)=
,分①当x0∈(-∞,0)及②当x0∈(0,π)时两种情况讨论函数值求出x0的值.
易推f[f(x0)]=0中f(x0)=
| π |
| 2 |
解答:
解:当x∈(-∞,0)时,∵f(x)=x2>0,
若f[f(x0)]=0,则f(x0)的函数值为0,不可能;
∴f(x0)∈(0,π)
∵cos
=0,∴f[f(x0)]=0中f(x0)=
,
①当x0∈(-∞,0)时,x02=
,∴x0=-
=-
,
②当x0∈(0,π)时,2cosx0=
,∴cosx0=
,∴x0=arccos
,
综上:x0=-
,或x0=arccos
,
故答案为:-
或arccos
.
若f[f(x0)]=0,则f(x0)的函数值为0,不可能;
∴f(x0)∈(0,π)
∵cos
| π |
| 2 |
| π |
| 2 |
①当x0∈(-∞,0)时,x02=
| π |
| 2 |
|
| ||
| 2 |
②当x0∈(0,π)时,2cosx0=
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
综上:x0=-
| ||
| 2 |
| π |
| 4 |
故答案为:-
| ||
| 2 |
| π |
| 4 |
点评:分段函数分段处理,这是研究分段函数图象和性质最核心的理念,具体做法是:根据自变量不同的分段,利用相应的函数表达式代换解题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知{an}是等差数列,a2+a4=10,a5+a7=22,则S6-S2等于( )
| A、26 | B、30 | C、32 | D、36 |
用反证法证明命题“若a>b,则
>
”时,假设的内容是( )
| 3 | a |
| 3 | b |
| A、a>b | ||||||
| B、a≤b | ||||||
C、
| ||||||
D、
|
集合M={x|x=sin
,k∈Z}中的元素有( )
| kπ |
| 3 |
| A、无数个 | B、4个 | C、3个 | D、2个 |
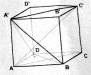 在正方体ABCD-A′B′C′D′中,求证:
在正方体ABCD-A′B′C′D′中,求证: