Question

设定义域为R的函数f（x）=

2-|x-1|+1，x≠1 a，x≠1

，若关于x的方程2f²（x）-（2a+3）f（x）+3a=0有五个不同的实数解，则a的取值范围是

 

．

Answer 1

考点：函数的零点与方程根的关系

专题：函数的性质及应用

分析：作出f（x）的图象，利用换元法结合一元二次函数的图象和性质即可．

解答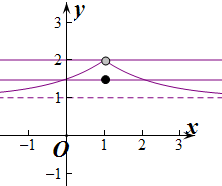： 解：作出f（x）的图象如图：设t=f（x），
则方程等价为2t²-（2a+3）t+3a=0，
由图象可知，
若关于x的方程2f²（x）-（2a+3）f（x）+3a=0有五个不同的实数解，
∴即要求对应于f（x）等于某个常数有3个不同实数解，
∴故先根据题意作出f（x）的简图：
由图可知，只有当f（x）=a时，它有三个根．
所以有：1＜a＜2 ①．
再根据2f²（x）-（2a+3）f（x）+3a=0有两个不等实根，
则判别式△=（2a+3）²-4×2×3a＞0，
解得a≠

3

2

，
故1＜a＜

3

2

或

3

2

＜x＜2，
故答案为：1＜a＜

3

2

或

3

2

＜x＜2

点评：本题主要考查函数和方程的应用，利用换元法结合一元二次函数的图象和性质，利用数形结合是解决本题的关键．