Question

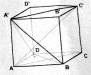在正方体ABCD-A′B′C′D′中，求证：
（1）平面ACC′A′⊥平面A′BD
（2）AC′⊥平面A′BD．

Answer 1

考点：平面与平面垂直的判定,直线与平面垂直的判定

专题：空间位置关系与距离

分析：（1）充分利用正方体的性质，容易得到BD⊥平面ACC′A′，利用面面垂直的判定定理可知；
（2）由正方体的性质得到A′D⊥平面AD′C′，进一步由线面垂直的性质得到A′D⊥AC′，同理得到A′B⊥AC′，由线面垂直的判定可得．

解答： 证明：（1）∵几何体是正方体的性质，
∴BD⊥AC，BD⊥AA′，
∴BD⊥平面ACC′A′，
∴平面ACC′A′⊥平面A′BD；
（2）连接 AD′，∵几何体是正方体，
∴A′D⊥AD′且C′D′⊥平面ADD′A′∴C′D′⊥A′D 
∴A′D⊥平面AD′C′
∴A′D⊥AC′
同理  A′B⊥AC′
则AC′⊥平面A′BD．

点评：本题考查了正方体的性质以及正方体中面面垂直的判定和线面垂直的判定，关键是熟练有关的判定定理和性质定理．本题也可以借助于向量解答．