题目内容
18．已知角α的终边与单位圆在第二象限交于点P（m，$\frac{4}{5}$）（1）求m的值
（2）求cos（α+$\frac{π}{4}$）
分析 （1）由题意可得：m2+（$\frac{4}{5}$）2=1，结合点P在第二象限，可求m的值．
（2）由三角函数定义可求cosα，sinα的值，进而利用两角和的余弦函数公式即可计算得解．
解答 （本题满分为10分）
解：（1）∵由题意可得：m2+（$\frac{4}{5}$）2=1，…（2分）
m=±$\frac{3}{5}$，…（3分）
∵点P在第二象限，
∴$m=-\frac{3}{5}$．…（5分）
（2）由三角函数定义可知，cosα=-$\frac{3}{5}$，sinα=$\frac{4}{5}$，…（7分）
可得：$cos（α+\frac{π}{4}）=cosαcos\frac{π}{4}-sinαsin\frac{π}{4}$…（8分）
=-$\frac{3}{5}×\frac{\sqrt{2}}{2}$-$\frac{4}{5}×\frac{\sqrt{2}}{2}$…（9分）
=-$\frac{7\sqrt{2}}{10}$．…（10分）
点评 本题主要考查了三角函数定义，两角和的余弦函数公式的应用，考查了数形结合思想，属于基础题．
练习册系列答案
相关题目
8．4个不同的小球全部随意放入3个不同的盒子里，使每个盒子都不空的放法种数为（ ）
| A． | C${\;}_{4}^{1}$C${\;}_{4}^{3}$C${\;}_{2}^{2}$ | B． | A${\;}_{3}^{1}$A${\;}_{4}^{3}$ | ||
| C． | C${\;}_{4}^{3}$A${\;}_{2}^{2}$ | D． | ${C}_{4}^{2}{A}_{3}^{3}$ |
9．函数f（x）是定义在R上的偶函数，且 f（2）=0，当x＞0时，有xf′（x）-f（x）＞0恒成立，则不等式f（x）＜0的解集为（ ）
| A． | （-∞，-2）∪（2，+∞） | B． | （-∞，-2）∪（0，2） | C． | （-2，0）∪（0，2） | D． | （-2，0）∪（2，+∞） |
6．下列函数中，图象的一部分符合右图的是（ ）
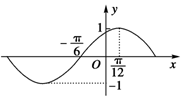
| A． | $y=sin（x+\frac{π}{6}）$ | B． | $y=sin（2x-\frac{π}{6}）$ | C． | $y=sin（2x+\frac{π}{6}）$ | D． | $y=sin（2x+\frac{π}{3}）$ |
一半径为4m的水轮（如图），水轮圆心O距离水面2m，已知水轮每分钟转动4圈，如果当水轮上点P从水中浮现时（图中点P0）开始计时．
3．欲证$\sqrt{2}-\sqrt{3}＜\sqrt{6}-\sqrt{7}$，只需证（ ）
| A． | ${（{\sqrt{2}+\sqrt{7}}）^2}＜{（{\sqrt{3}+\sqrt{6}}）^2}$ | B． | ${（{\sqrt{2}-\sqrt{6}}）^2}＜{（{\sqrt{3}-\sqrt{7}}）^2}$ | C． | ${（{\sqrt{2}-\sqrt{3}}）^2}＜{（{\sqrt{6}-\sqrt{7}}）^2}$ | D． | ${（{\sqrt{2}-\sqrt{3}-\sqrt{6}}）^2}＜{（{-\sqrt{7}}）^2}$ |
如图，四棱锥P-ABCD，底面ABCD是边长为2的菱形，$∠ABC=\frac{π}{3}$，且PA⊥平面ABCD．