题目内容
10.设a>0,b>0,且a+b=$\frac{1}{a}$+$\frac{1}{b}$.证明:(1)设$M=\frac{1}{a+1}+\frac{1}{b+1}$,$N=\frac{a}{a+1}+\frac{b}{b+1}$,求证M=N
(2)a2+a<2与b2+b<2不可能同时成立.
分析 (1)利用已知条件求出ab=1,然后利用1的代换,化简N推出等于M即可.
(2)利用反证法,假设a2+a<2与b2+b<2同时成立,推出ab<1,这与ab=1矛盾,说明不等式成立.
解答 证明:(1)由a+b=$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$,a>0,b>0,得ab=1.
$N=\frac{a}{a+1}+\frac{b}{b+1}$=$\frac{a}{a+ab}+\frac{b}{b+ab}$=$\frac{1}{b+1}+\frac{1}{a+1}$=M
所以得证M=N…(5分)
(2)假设a2+a<2与b2+b<2同时成立,
则由a2+a<2及a>0得0<a<1;
同理,0<b<1,从而ab<1,这与ab=1矛盾.
故a2+a<2与b2+b<2不可能同时成立…(10分)
点评 本题考查等式以及不等式的证明,反证法的应用,考查转化思想以及计算能力.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
20.在△ABC中,已知a=5,b=5$\sqrt{3}$.C=30°,则角C的对边c的长为( )
| A. | 5$\sqrt{13}$ | B. | 5$\sqrt{11}$ | C. | 5$\sqrt{7}$ | D. | 5 |
5.如果复数z满足|z+1-i|=2,那么|z-2+i|的最大值是( )
| A. | $\sqrt{13}+2$ | B. | $2+\sqrt{3}i$ | C. | $\sqrt{13}+\sqrt{2}$ | D. | $\sqrt{13}+4$ |
15.若$tanθ=\frac{1}{2}$,则cos2θ+sin2θ=( )
| A. | $\frac{4}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{8}{5}$ | D. | 2 |
19.一袋子中装有100个大小相同的红球、白球和黑球,其中45个红球,从中摸出一个球,摸出白球的概率为0.23,则摸出黑球的概率为( )
| A. | 0.35 | B. | 0.32 | C. | 0.55 | D. | 0.68 |
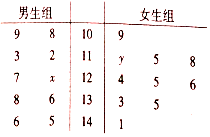 在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图:
在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图: