题目内容
已知n∈(0,1),函数f(x)=x2+x+n有零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:求出函数f(x)有零点时对应的区域长度的大小,n∈(0,1)对应的区域长度的大小,再代入几何概型的计算公式进行解答.
解答:
解:∵函数f(x)=x2+x+n有零点,
∴△=1-4n≥0,
∴n≤
,
∵n∈(0,1),
∴n∈(0,
],
∴函数f(x)=x2+x+n有零点的概率为
=
.
故选B.
∴△=1-4n≥0,
∴n≤
| 1 |
| 4 |
∵n∈(0,1),
∴n∈(0,
| 1 |
| 4 |
∴函数f(x)=x2+x+n有零点的概率为
| ||
| 1 |
| 1 |
| 4 |
故选B.
点评:本题考查了几何概型、二次函数的零点.几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a>b>0,则下列结论正确的是( )
| A、a2<b2 |
| B、ab<b2 |
| C、a+b>2b |
| D、a-b>a+b |
(文)Sn=1-2+3-4+5-6+…+(-1)n+1•n,则S100+S200+S301等于( )
| A、1 | B、-1 | C、51 | D、52 |
设x+x-1=3,则x3+x-3的值为( )
| A、18 | B、±6 | C、12 | D、6 |
关于x的不等式
≥0的解为-1≤x<2或x≥3,则点P(a+b,c)位于( )
| (x-a)(x-b) |
| x-c |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
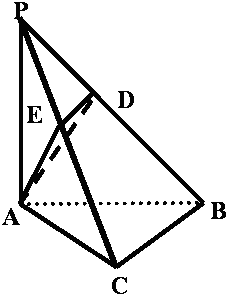 如图,在三梭锥P-ABC中,PA⊥底面ABC,PA=AB=2,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC
如图,在三梭锥P-ABC中,PA⊥底面ABC,PA=AB=2,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC