题目内容
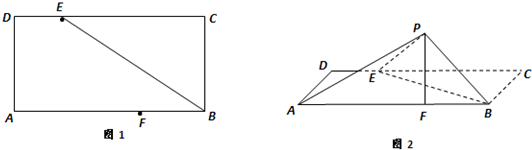
如图,边长为3的正方形ABCD中
(1)点E、F分别是AB、BC上的点,将△BEF,△AED,△DCF分别沿EF、DE、DF折起,使A、B、C三点重合于点P,求PD与平面EFD所成角的正弦值;
(2)当BE=BF=
BC时,将△AED,△DCF分别沿DE、DF折起,使A、C两点重合于点Q,求点E到平面QDF的距离.
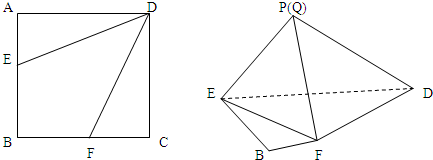
(1)点E、F分别是AB、BC上的点,将△BEF,△AED,△DCF分别沿EF、DE、DF折起,使A、B、C三点重合于点P,求PD与平面EFD所成角的正弦值;
(2)当BE=BF=
| 1 |
| 3 |

考点:直线与平面所成的角,点、线、面间的距离计算
专题:计算题,空间位置关系与距离,空间角
分析:(1)为了找到PD与平面EFD所成角,需找到过点P且垂直于面EFD的垂线.由于PE=PF、DE=DF,故可取EF中点G,连DG、PG,作PH⊥DG于H,证出PH⊥平面EFD,可得PD与平面EFD所成角为∠PDG,然后在Rt△PDG中加以计算,可得PD与平面EFD所成角的正弦值;
(2)根据等体积法利用VE-PDF=VD-PEF,结合题意即可算出点E到平面QDF的距离.
(2)根据等体积法利用VE-PDF=VD-PEF,结合题意即可算出点E到平面QDF的距离.
解答:
解:(1)∵DP⊥PF,DP⊥PE,PE、PF是平面PEF内的相交直线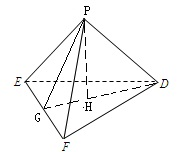
∴DP⊥平面PEF,结合EF?平面PEF可得PD⊥EF.
取EF中点G,连经PG、DG,作PH⊥DG于H,
∵E、F为中点,可得△ADE≌△CDF,
∴DE=DF,从而DG⊥EF
同理可得EF⊥PG
又∵PG∩DG=G,∴EF⊥平面PDG,故EF⊥PH,从而PH⊥平面DEF
∴PD与平面EFD所成角为∠PDG
∵正方形ABCD边长为3,∴PD=3,DE=DF=
,EF=
,DG=
在Rt△PDG中,cos∠PDG=
=
=
,可得sin∠PDG=
=
;
(1)由(1)的证明,可得DP⊥平面PEF,
∵△PEF中,PE=PF=
BC=2,EF=
,∴S△PEF=
×
×
=
,
直角△PDF的面积为S△PDF=
×3×2=3
设点E到平面QDF的距离为d,由VE-PDF=VD-PEF,可得
×S△PDF×d=
×S△PEF×PD,
即
×3×d=
×
×3,解得d=
,即点E到平面QDF的距离为
.

∴DP⊥平面PEF,结合EF?平面PEF可得PD⊥EF.
取EF中点G,连经PG、DG,作PH⊥DG于H,
∵E、F为中点,可得△ADE≌△CDF,
∴DE=DF,从而DG⊥EF
同理可得EF⊥PG
又∵PG∩DG=G,∴EF⊥平面PDG,故EF⊥PH,从而PH⊥平面DEF
∴PD与平面EFD所成角为∠PDG
∵正方形ABCD边长为3,∴PD=3,DE=DF=
3
| ||
| 2 |
3
| ||
| 2 |
9
| ||
| 4 |
在Rt△PDG中,cos∠PDG=
| PD |
| DF |
| 3 | ||||
|
2
| ||
| 3 |
| 1-cos2∠PDG |
| 1 |
| 3 |
(1)由(1)的证明,可得DP⊥平面PEF,
∵△PEF中,PE=PF=
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 2 |
4-
|
| ||
| 2 |
直角△PDF的面积为S△PDF=
| 1 |
| 2 |
设点E到平面QDF的距离为d,由VE-PDF=VD-PEF,可得
| 1 |
| 3 |
| 1 |
| 3 |
即
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题给出平面图形的翻折,求线面所成的角并求点到平面的距离.着重考查了空间的垂直位置关系的判定与应用、用等体积法求点到平面的距离等知识,属于中档题.

练习册系列答案
相关题目
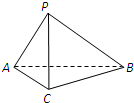 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.