题目内容
某工厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量P(mg/L)与时间t(小时)间的关系为P=P0e-kt.如果在前5个小时消除了10%的污染物,试求:
(1)10个小时后还剩百分之几的污染物?
(2)污染物减少50%所需要的时间.(参考数据:ln2=0.7,ln3=1.1,ln5=1.6)
(1)10个小时后还剩百分之几的污染物?
(2)污染物减少50%所需要的时间.(参考数据:ln2=0.7,ln3=1.1,ln5=1.6)
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)由5小时后剩留的污染物列等式求出P=P0e-kt中k的值,得到具体关系式后代t=10求得10个小时后还剩污染物的百分数;
(2)由污染物减少50%,即P=50%P0列等式50%P0=P0e(
ln0.9)t求解污染物减少50%所需要的时间.
(2)由污染物减少50%,即P=50%P0列等式50%P0=P0e(
| 1 |
| 5 |
解答:
解:(1)由P=P0e-kt,可知,当t=0时,P=P0;
当t=5时,P=(1-10%)P0.于是有
(1-10%)P0=P0e-5k,解得k=-
ln0.9,那么P=P0e(
ln0.9)t,
∴当t=10时,P=P0e(
ln0.9)×10=P0eln0.81=81%P0.
∴10个小时后还剩81%的污染物;
(2)当P=50%P0时,有50%P0=P0e(
ln0.9)t,
解得t=
=
=5•
=5•
=35.
∴污染物减少50%所需要的时间为35个小时.
当t=5时,P=(1-10%)P0.于是有
(1-10%)P0=P0e-5k,解得k=-
| 1 |
| 5 |
| 1 |
| 5 |
∴当t=10时,P=P0e(
| 1 |
| 5 |
∴10个小时后还剩81%的污染物;
(2)当P=50%P0时,有50%P0=P0e(
| 1 |
| 5 |
解得t=
| ln0.5 | ||
|
5ln
| ||
ln
|
| -ln2 |
| ln9-ln10 |
| ln2 |
| ln2+ln5-2ln3 |
∴污染物减少50%所需要的时间为35个小时.
点评:本题考查了函数模型的选择及应用,关键是对题意的理解,由题意正确列出相应的等式,考查了计算能力,是中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
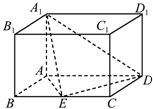 如图,长方体ABCD-A1B1C1D1中,E为线段BC的中点,AB=1,AD=2,AA1=
如图,长方体ABCD-A1B1C1D1中,E为线段BC的中点,AB=1,AD=2,AA1=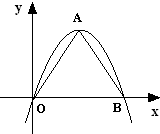 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.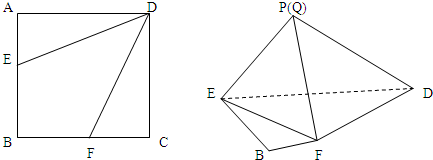
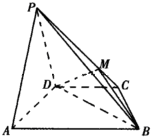 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,在锐角△PAD中PA=PD,并且BD=2AD=8,
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,在锐角△PAD中PA=PD,并且BD=2AD=8, (几何证明选讲选做题) 如图,∠ACB=90°,AC是圆O的切线,切点为E,割线ADB过圆心O,若
(几何证明选讲选做题) 如图,∠ACB=90°,AC是圆O的切线,切点为E,割线ADB过圆心O,若