题目内容
对于给定的以下四个命题:
①函数f(x)=
是奇函数;
②函数f(x)在(a,b)和(c,d)都是增函数,若x1∈(a,b),x2∈(c,d),且x1<x2则一定有f(x1)<f(x2);
③函数f(x)在R上为奇函数,且当x>0时有f(x)=
+1,则当x<0,f(x)=-
-1;
④函数y=x+
的值域为{y|y≤1}.
其中正确命题的序号是 .
①函数f(x)=
| x2-2x |
| x-2 |
②函数f(x)在(a,b)和(c,d)都是增函数,若x1∈(a,b),x2∈(c,d),且x1<x2则一定有f(x1)<f(x2);
③函数f(x)在R上为奇函数,且当x>0时有f(x)=
| x |
| -x |
④函数y=x+
| 1-2x |
其中正确命题的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①求出函数f(x)=
的定义域,即可判定f(x)不是奇函数;
②举例说明命题不成立即可;
③由题意,利用奇偶性以及x>0时f(x)的解析式,求出x<0时f(x)的解析式;
④用换元法,设t=
,求出函数y在某一区间上的最值即得值域.
| x2-2x |
| x-2 |
②举例说明命题不成立即可;
③由题意,利用奇偶性以及x>0时f(x)的解析式,求出x<0时f(x)的解析式;
④用换元法,设t=
| 1-2x |
解答:
解:①∵函数f(x)=
的定义域是{x|x≠2},不关于原点对称,
∴f(x)是非奇非偶的函数,
∴命题①错误;
②当f(x)=-
时,f(x)在(-∞0)(0+∞)上都是增函数,
且-1<1,但f(-1)=1,f(1)=-1,
∴命题②错误;
③根据题意,当x<0时,-x>0,
∴f(-x)=
+1;
又f(x)在R上是奇函数,
∴f(-x)=-f(x),
∴f(x)=-f(-x)=-
-1,
∴命题③正确;
④设t=
,∴x=
(1-t2),(其中t≥0);
∴函数可化为y=
(1-t2)+t=-
t2+t+
=-
(t-1)2+1,
∵t≥0,∴当t=1时,y有最大值1;
∴函数y的值域为{y|y≤1}.
所以,以上正确的命题序号为③④;
故答案为:③④.
| x2-2x |
| x-2 |
∴f(x)是非奇非偶的函数,
∴命题①错误;
②当f(x)=-
| 1 |
| x |
且-1<1,但f(-1)=1,f(1)=-1,
∴命题②错误;
③根据题意,当x<0时,-x>0,
∴f(-x)=
| -x |
又f(x)在R上是奇函数,
∴f(-x)=-f(x),
∴f(x)=-f(-x)=-
| -x |
∴命题③正确;
④设t=
| 1-2x |
| 1 |
| 2 |
∴函数可化为y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵t≥0,∴当t=1时,y有最大值1;
∴函数y的值域为{y|y≤1}.
所以,以上正确的命题序号为③④;
故答案为:③④.
点评:本题通过命题真假的判定,考查了函数的奇偶性与单调性以及求函数的值域问题,是综合题.

练习册系列答案
相关题目
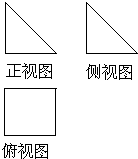 一几何体的三视图如图所示,若正视图和侧视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )
一几何体的三视图如图所示,若正视图和侧视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )A、
| ||
| B、2π | ||
| C、3π | ||
| D、12π |