题目内容
下列7个判断:
①若f(x)=x2-2ax在[1,+∞)上增函数,则a=1;②函数f(x)=2x-x2只有两个零点;
③函数y=ln(x2+1)的值域是R;④函数y=2|x|的最小值是1;⑤在同一坐标系中函数y=2x与y=2-x的图象关于y轴对称;⑥设a>1,log0.2a、0.2a、a0.2的大小关系为log0.2a<0.2a<a0.2;⑦设偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是增函数,则f(-2),f(π),f(-3)的大小关为U=R;
其中正确的序号为 .
①若f(x)=x2-2ax在[1,+∞)上增函数,则a=1;②函数f(x)=2x-x2只有两个零点;
③函数y=ln(x2+1)的值域是R;④函数y=2|x|的最小值是1;⑤在同一坐标系中函数y=2x与y=2-x的图象关于y轴对称;⑥设a>1,log0.2a、0.2a、a0.2的大小关系为log0.2a<0.2a<a0.2;⑦设偶函数f(x)的定义域为R,当x∈[0,+∞)时,f(x)是增函数,则f(-2),f(π),f(-3)的大小关为U=R;
其中正确的序号为
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①由f(x)是二次函数,根据二次函数的图象与性质,判定函数的单调区间即可;
②在同一坐标系内画出函数y=2x,y=x2的图象,由图象交点的个数判定f(x)的零点个数;
③由x2≥0,求出函数y=ln(x2+1)的值域即可;
④由|x|≥0,求出函数y=2|x|的最小值即可;
⑤由f(x)=2|x|是R上的偶函数,判定函数y=2x与y=2-x的对称问题即可;
⑥当a>1时,由指数函数、对数函数的图象与性质判定log0.2a、0.2a与a0.2的大小即可;
⑦由f(x)是偶函数且在[0,+∞)上是增函数,可以判定f(-2)、f(-3)与f(π)的大小.
②在同一坐标系内画出函数y=2x,y=x2的图象,由图象交点的个数判定f(x)的零点个数;
③由x2≥0,求出函数y=ln(x2+1)的值域即可;
④由|x|≥0,求出函数y=2|x|的最小值即可;
⑤由f(x)=2|x|是R上的偶函数,判定函数y=2x与y=2-x的对称问题即可;
⑥当a>1时,由指数函数、对数函数的图象与性质判定log0.2a、0.2a与a0.2的大小即可;
⑦由f(x)是偶函数且在[0,+∞)上是增函数,可以判定f(-2)、f(-3)与f(π)的大小.
解答:
解:①当f(x)=x2-2ax在[1,+∞)上是增函数时,
二次函数图象的对称轴x=a≤1,
∴命题①错误;
②考查函数y=2x,y=x2的图象,如图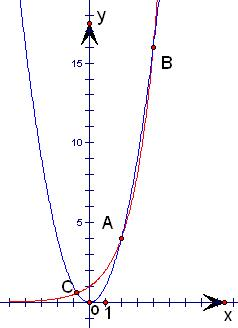 ,
,
由图象知两函数有3个交点,
∴f(x)=2x-x2有3个零点,
∴命题②错误;
③∵x2≥0,
∴x2+1≥1,
∴ln(x2+1)≥0;
∴函数y=ln(x2+1)的值域是[0,+∞);
∴③错误;
④∵|x|≥0,
∴2|x|≥20=1,
∴函数y=2|x|的最小值是1;
∴命题④正确;
⑤∵f(x)=2|x|,是R上的偶函数,图象关于y轴对称,
∴在同一坐标系中,函数y=2x与y=2-x的图象关于y轴对称,
∴命题⑤正确;
⑥∵a>1,
∴log0.2a<log0.21=0,
0<0.2a<0.21=0.2,
1=a0<a0.2,
∴log0.2a<0.2a<a0.2;
∴命题⑥正确;
⑦∵偶函数f(x)的定义域为R,
∴f(-2)=f(2),
f(-3)=f(3),
当x∈[0,+∞)时,f(x)是增函数,
∴f(2)<f(3)<f(π),
∴f(-2)<f(-3)<f(π),
∴命题⑦错误;
所以,以上命题正确的是④⑤⑥;
故答案为:④⑤⑥.
二次函数图象的对称轴x=a≤1,
∴命题①错误;
②考查函数y=2x,y=x2的图象,如图
 ,
,由图象知两函数有3个交点,
∴f(x)=2x-x2有3个零点,
∴命题②错误;
③∵x2≥0,
∴x2+1≥1,
∴ln(x2+1)≥0;
∴函数y=ln(x2+1)的值域是[0,+∞);
∴③错误;
④∵|x|≥0,
∴2|x|≥20=1,
∴函数y=2|x|的最小值是1;
∴命题④正确;
⑤∵f(x)=2|x|,是R上的偶函数,图象关于y轴对称,
∴在同一坐标系中,函数y=2x与y=2-x的图象关于y轴对称,
∴命题⑤正确;
⑥∵a>1,
∴log0.2a<log0.21=0,
0<0.2a<0.21=0.2,
1=a0<a0.2,
∴log0.2a<0.2a<a0.2;
∴命题⑥正确;
⑦∵偶函数f(x)的定义域为R,
∴f(-2)=f(2),
f(-3)=f(3),
当x∈[0,+∞)时,f(x)是增函数,
∴f(2)<f(3)<f(π),
∴f(-2)<f(-3)<f(π),
∴命题⑦错误;
所以,以上命题正确的是④⑤⑥;
故答案为:④⑤⑥.
点评:本题通过命题真假的判定考查了对称轴,单调性与奇偶性,以及利用单调性比较函数值的大小问题,是综合题目.

练习册系列答案
相关题目
下列说法正确的是( )
| A、梯形可以确定一个平面 |
| B、圆心和圆上两点可以确定一个平面 |
| C、两条直线a,b没有公共点,那么a与b是异面直线 |
| D、若a,b是两条直线,α,β是两个平面,且a?α,b?β,则a,b是异面直线 |