题目内容
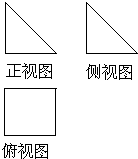一几何体的三视图如图所示，若正视图和侧视图都是等腰直角三角形，直角边长为1，则该几何体外接球的表面积为（ ）A、
| ||
| B、2π | ||
| C、3π | ||
| D、12π |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：根据三视图判断几何体为四棱锥，利用四棱锥补全正方体，即四棱锥的外接球即是边长为1的正方体的外接球，由此可得外接球的直径为
，代入球的表面积公式计算．
| 3 |
解答：
解：由三视图知几何体为三棱锥D1-ABC，
∴三棱锥的外接球即是边长为1的正方体的外接球，∴外接球的直径为
，
∴外接球的表面积S=4π×(
)2=3π．
故选：C．
∴三棱锥的外接球即是边长为1的正方体的外接球，∴外接球的直径为
| 3 |
∴外接球的表面积S=4π×(
| ||
| 2 |
故选：C．
点评：本题考查由三视图求几何体外接球的表面积，解答此类问题的关键是根据数据所对应的几何量求得相关几何量的数据．
练习册系列答案
阅读快车系列答案
相关题目
若双曲线C：2x2-y2=m（m＞0）与抛物线y2=8x的准线交于A，B两点，且|AB|=2
，则实数m的值为（ ）
| 3 |
| A、29 | B、20 | C、12 | D、5 |
已知函数f(x)=x+
，则函数y=f（x）的大致图象为（ ）
| ln|x| |
| x |
A、 |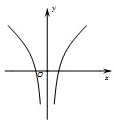
B、 |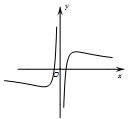
C、 |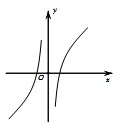
D、 |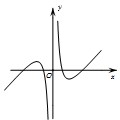
下列说法正确的是（ ）
| A、梯形可以确定一个平面 |
| B、圆心和圆上两点可以确定一个平面 |
| C、两条直线a，b没有公共点，那么a与b是异面直线 |
| D、若a，b是两条直线，α，β是两个平面，且a?α，b?β，则a，b是异面直线 |
实数x，y满足
则z=x-3y的最小值为（ ）
|
| A、-2 | ||
| B、-1 | ||
C、
| ||
| D、2 |
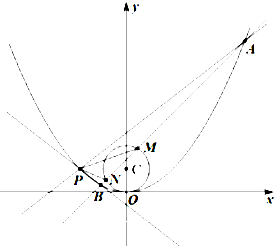设点P（-2，1）在抛物线x2=2py（p＞0）上，且到圆C：x2+（y+b）2=1上点的最小距离为1．