题目内容
13.若x,y满足约束条件$\left\{\begin{array}{l}{x+y≤0}\\{x-y≤0}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$,则z=$\frac{y-2}{x+3}$的最小值为( )| A. | -2 | B. | -$\frac{2}{3}$ | C. | -$\frac{12}{5}$ | D. | $\frac{\sqrt{2}-4}{7}$ |
分析 由约束条件作出可行域,由z=$\frac{y-2}{x+3}$的几何意义,即可行域内的动点与定点P(-3,2)连线的斜率,结合直线与圆的位置关系求得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y≤0}\\{x-y≤0}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$作出可行域如图,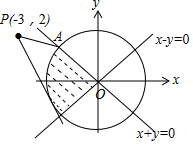
z=$\frac{y-2}{x+3}$的几何意义为可行域内的动点与定点P(-3,2)连线的斜率.
设过P的圆的切线的斜率为k,则切线方程为y-2=k(x+3),即kx-y+3k+2=0.
由$\frac{|3k+2|}{\sqrt{{k}^{2}+1}}=2$,解得k=0或k=-$\frac{12}{5}$.
∴z=$\frac{y-2}{x+3}$的最小值为-$\frac{12}{5}$.
故选;C.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
3.如果函数y=logax(a>0且a≠1)在[1,3]上的最大值与最小值的差为2,则满足条件的a值的集合是( )
| A. | $\{\sqrt{3}\}$ | B. | $\{\frac{{\sqrt{3}}}{3}\}$ | C. | $\{\frac{{\sqrt{3}}}{3},\sqrt{3}\}$ | D. | $\{\sqrt{3},3\}$ |
4.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$(a>0,b>0)的右焦点为F,过点F作x轴的垂线与双曲线交于B,C两点(点B在x轴上方),过点B作斜率为负数的渐近线的垂线,过点C作斜率为正数的渐近线的垂线,两垂线交于点D,若D到直线BC的距离等于虚轴长,则双曲线的离心率e等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
1.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≤a}\\{y≥0}\end{array}\right.$,若目标函数z=2x+y的最大值为4,则实数a=( )
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
18.若(2x+1)n=a0+a1x+a2x2+…+anxn的展开式中的各项系数和为243,则a1+2a2+…+nan=( )
| A. | 405 | B. | 810 | C. | 243 | D. | 64 |
5.已知角α终边上一点P(-3,4),则cos(-π-α)的值为( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
2.甲、乙两人约定晚6点到晚7点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率( )
| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
