题目内容
3.已知直线AB:x+y-6=0与抛物线y=x2及x轴正半轴围成的图形为Ω,若从Rt△AOB区域内任取一点M(x,y),则点M取自图形Ω的概率为$\frac{16}{27}$.分析 欲求所投的点落在阴影内部的概率,利用几何概型解决,只须利用定积分求出阴影图的面积,最后利用它们的面积比求得即可概率.
解答 解:由定积分可求得阴影部分图形Ω的面积为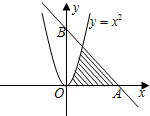 :
:
S=∫02x2dx+∫26(6-x)dx
=$\frac{1}{3}{x}^{3}{|}_{0}^{2}+(6x-\frac{1}{2}{x}^{2}){|}_{2}^{6}$=$\frac{32}{3}$,
又Rt△AOB的面积为:$\frac{1}{2}×6×6$=18
所以P=$\frac{\frac{32}{3}}{18}$=$\frac{16}{27}$.
故答案为:$\frac{16}{27}$.
点评 本题考查了利用定积分求面积以及几何摡型知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
13.若x,y满足约束条件$\left\{\begin{array}{l}{x+y≤0}\\{x-y≤0}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$,则z=$\frac{y-2}{x+3}$的最小值为( )
| A. | -2 | B. | -$\frac{2}{3}$ | C. | -$\frac{12}{5}$ | D. | $\frac{\sqrt{2}-4}{7}$ |
15.已知函数f(x)=2sin($\frac{x+φ}{2}$)cos($\frac{x+φ}{2}$)(|φ|<$\frac{π}{2}$),且对任意的x∈R,f(x)≤f($\frac{π}{6}$),则( )
| A. | f(x)=f(x+π) | B. | f(x)=f(x+$\frac{π}{2}$) | C. | f(x)=f($\frac{π}{3}$-x) | D. | f(x)=f($\frac{π}{6}$-x) |
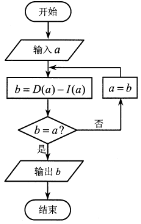 设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746,
设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746,