题目内容
5.已知角α终边上一点P(-3,4),则cos(-π-α)的值为( )| A. | -$\frac{4}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
分析 利用任意角的三角函数的定义,诱导公式,求得cos(-π-α)的值.
解答 解:∵角α终边上一点P(-3,4),∴cosα=$\frac{-3}{5}$=-$\frac{3}{5}$,
则cos(-π-α)=cos(π-α)=-cosα=$\frac{3}{5}$,
故选:C.
点评 本题主要考查任意角的三角函数的定义,诱导公式,属于基础题.

练习册系列答案
相关题目
13.若x,y满足约束条件$\left\{\begin{array}{l}{x+y≤0}\\{x-y≤0}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$,则z=$\frac{y-2}{x+3}$的最小值为( )
| A. | -2 | B. | -$\frac{2}{3}$ | C. | -$\frac{12}{5}$ | D. | $\frac{\sqrt{2}-4}{7}$ |
20.集合A={1,3,5,7},B={x|x2-4x≤0},则A∩B=( )
| A. | (1,3) | B. | {1,3} | C. | (5,7) | D. | {5,7} |
17.在平面直角坐标系中,不等式组$\left\{\begin{array}{l}{x+y≤0}\\{x-y≤0}\\{{x}^{2}+{y}^{2}≤{r}^{2}}\end{array}\right.$(r为常数)表示的平面区域的面积为π,若x,y满足上述约束条件,则z=$\frac{x+y+1}{x+3}$的最小值为( )
| A. | -1 | B. | -$\frac{5\sqrt{2}+1}{7}$ | C. | $\frac{1}{3}$ | D. | -$\frac{7}{5}$ |
15.已知函数f(x)=2sin($\frac{x+φ}{2}$)cos($\frac{x+φ}{2}$)(|φ|<$\frac{π}{2}$),且对任意的x∈R,f(x)≤f($\frac{π}{6}$),则( )
| A. | f(x)=f(x+π) | B. | f(x)=f(x+$\frac{π}{2}$) | C. | f(x)=f($\frac{π}{3}$-x) | D. | f(x)=f($\frac{π}{6}$-x) |
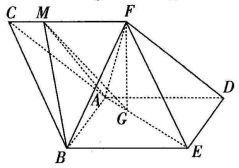 如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=$\frac{π}{3}$,BC=$\frac{\sqrt{21}}{2}$,四棱锥F-ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM=$\frac{1}{4}$CF.
如图,三棱柱ABC-DEF中,侧面ABED是边长为2的菱形,且∠ABE=$\frac{π}{3}$,BC=$\frac{\sqrt{21}}{2}$,四棱锥F-ABED的体积为2,点F在平面ABED内的正投影为G,且G在AE上,点M是在线段CF上,且CM=$\frac{1}{4}$CF.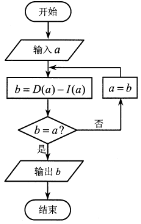 设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746,
设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746,