题目内容
1．设变量x，y满足约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≤a}\\{y≥0}\end{array}\right.$，若目标函数z=2x+y的最大值为4，则实数a=（ ）| A． | 2 | B． | 3 | C． | -2 | D． | -3 |
分析 作出可行域，变形目标函数并平移直线y=-2x，作出最优解，代入方程求解a可得结论．
解答 
解：作出约束条件$\left\{\begin{array}{l}{x-y≥0}\\{x+y≤a}\\{y≥0}\end{array}\right.$，所对应的可行域（如图阴影三角形），
目标函数z=2x+y可化为y=-2x+z，平移直线y=-2x可知，
当直线经过点A（2，0）时，
截距z取最大值，
∴（2，0）在直线x+y=a上，解得a=2，
故选：A．
点评 本题考查简单线性规划，准确作图是解决问题的关键，属中档题．
练习册系列答案
相关题目
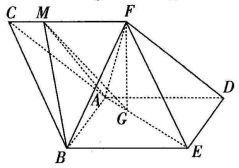如图，三棱柱ABC-DEF中，侧面ABED是边长为2的菱形，且∠ABE=$\frac{π}{3}$，BC=$\frac{\sqrt{21}}{2}$，四棱锥F-ABED的体积为2，点F在平面ABED内的正投影为G，且G在AE上，点M是在线段CF上，且CM=$\frac{1}{4}$CF．
13．若x，y满足约束条件$\left\{\begin{array}{l}{x+y≤0}\\{x-y≤0}\\{{x}^{2}+{y}^{2}≤4}\end{array}\right.$，则z=$\frac{y-2}{x+3}$的最小值为（ ）
| A． | -2 | B． | -$\frac{2}{3}$ | C． | -$\frac{12}{5}$ | D． | $\frac{\sqrt{2}-4}{7}$ |