题目内容
若f(x)满足f(x)+f(-x)=0,且对任意x∈R都有f(x+5)=f(x)成立,又f(1)=1,f(2)=-3,则f(3)+f(4)= .
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:对任意x∈R都有f(x+5)=f(x)成立,则f(x)以5为最小正周期的函数,再由f(x)+f(-x)=0,得到
f(3)+f(4)=-f(2)-f(1),代入数据,即可得到答案.
f(3)+f(4)=-f(2)-f(1),代入数据,即可得到答案.
解答:
解:f(x)满足f(x)+f(-x)=0,
则f(-x)=-f(x),
对任意x∈R都有f(x+5)=f(x)成立,
则f(x)以5为最小正周期的函数,
则f(3)+f(4)=f(3-5)+f(4-5)
=f(-2)+f(-1)=-f(2)-f(1)
又f(1)=1,f(2)=-3,
则f(3)+f(4)=3-1=2.
故答案为:2.
则f(-x)=-f(x),
对任意x∈R都有f(x+5)=f(x)成立,
则f(x)以5为最小正周期的函数,
则f(3)+f(4)=f(3-5)+f(4-5)
=f(-2)+f(-1)=-f(2)-f(1)
又f(1)=1,f(2)=-3,
则f(3)+f(4)=3-1=2.
故答案为:2.
点评:本题考查函数的奇偶性和周期性及运用,考查运算能力,属于中档题和易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
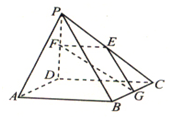 如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.
如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.