题目内容
对于函数f(x),若存在x0∈R,使方程f(x0)=x0成立,则称x0为f(x)的不动点,已知函数f(x)=ax2+(b+1)x+b-1.
(1)当a=1,b=-2时,求f(x)的不动点;
(2)当b=2时,若函数f(x)存在不动点x0∈(-1,1),求实数a的取值范围.
(1)当a=1,b=-2时,求f(x)的不动点;
(2)当b=2时,若函数f(x)存在不动点x0∈(-1,1),求实数a的取值范围.
考点:二次函数的性质,函数的值
专题:函数的性质及应用
分析:(1)将a、b代入函数,根据条件“若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点”建立方程解之即可;
(2)将b=2代入得到ax2+2x+1=0,令g(x)=ax2+2x+1,通过讨论a=0,a≠0得出结论.
(2)将b=2代入得到ax2+2x+1=0,令g(x)=ax2+2x+1,通过讨论a=0,a≠0得出结论.
解答:
解:(1)当a=1,b=-2时,f(x)=x2-x-3=x?x2-2x-3=0?(x-3)(x+1)=0?x=3或x=-1,
∴f(x)的不动点为x=3或x=-1.
(2)b=2时,f(x)=ax2+3x+1=x,
∴ax2+2x+1=0,
令g(x)=ax2+2x+1,
a=0时,令g(x)=0,解得:x=-
,符合题意,
a≠0时,由题意得:g(x)在(-1,1)上有零点,
∴g(-1)g(1)<0,即(a-1)(a+3)<0,解得:-3<a<1,且a≠0,
综上:-3<a<1.
∴f(x)的不动点为x=3或x=-1.
(2)b=2时,f(x)=ax2+3x+1=x,
∴ax2+2x+1=0,
令g(x)=ax2+2x+1,
a=0时,令g(x)=0,解得:x=-
| 1 |
| 2 |
a≠0时,由题意得:g(x)在(-1,1)上有零点,
∴g(-1)g(1)<0,即(a-1)(a+3)<0,解得:-3<a<1,且a≠0,
综上:-3<a<1.
点评:本题主要考查了函数与方程的综合运用,考查了转化思想,考查了函数的零点问题,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
=(1,2),
=(2,3),则λ<-4是向量
=λ
+
与向量
=(3,-1)夹角钝角的( )
| a |
| b |
| m |
| a |
| b |
| n |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要的条件 |
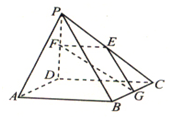 如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.
如图,在四棱锥P-ABCD中,PD⊥ABCD,ABCD为正方形.AD=PD=2,E,F,GPC,PD,CB,AP∥EGF,求二面角G-EF-D的大小.