题目内容
在△ABC中,a、b、c分别是角A、B、C的对边,
=(2a+c,b),
=(cosB,cosC),且
⊥
.
(1)求角B的大小;
(2)设f(x)=2sinxcosxcos(A+C)-
cos2x,如果当x∈[0,
]时,不等式f(x)+λ≥0恒成立,求λ的最小值;
(3)在(2)的条件下,若将f(x)图象向左平移t(t>0)个单位后,所得图象为偶函数图象;将f(x)图象向右平移s(s>0)个单位后,所得图象为奇函数图象,求s+t的最小值.
| m |
| n |
| m |
| n |
(1)求角B的大小;
(2)设f(x)=2sinxcosxcos(A+C)-
| ||
| 2 |
| π |
| 2 |
(3)在(2)的条件下,若将f(x)图象向左平移t(t>0)个单位后,所得图象为偶函数图象;将f(x)图象向右平移s(s>0)个单位后,所得图象为奇函数图象,求s+t的最小值.
考点:函数y=Asin(ωx+φ)的图象变换,平面向量数量积的运算,两角和与差的正弦函数
专题:三角函数的图像与性质
分析:(1)根据向量垂直的坐标关系,即可求角B的大小;
(2)利用辅助角公式将f(x)进行化简将不等式f(x)+λ≥0进行转化,求函数的最值即可求λ的最小值;
(3)根据三角函数的平移关系结合三角函数的奇偶性求出s,t的最小值即可得到结论.
(2)利用辅助角公式将f(x)进行化简将不等式f(x)+λ≥0进行转化,求函数的最值即可求λ的最小值;
(3)根据三角函数的平移关系结合三角函数的奇偶性求出s,t的最小值即可得到结论.
解答:
解:(1)∵
=(2a+c,b),
=(cosB,cosC),且
⊥
.
∴(2a+c)cosB+bcosC=0,
即2acosB+ccosB+bcosC=0,
由正弦定理得2sinAcosB+sinCcosB+cosCsinB=0,
即2sinAcosB+sin(C+B)=0,
∴sinA(2cosB+1)=0,
在三角形中,2cosB+1=0,即cosB=-
,解得B=
.
(2)∵B=
,∴A+C=
,
f(x)=
sin2x-
cos2x=sin(2x-
),
当x∈[0,
]时,-
≤2x-
≤
,
-
≤sin(2x-
)≤1,
要使f(x)+λ≥0恒成立,
即f(x)≥-λ,
则-λ≥-
,
即λ≤
,即λ的最小值是
.
(3)将f(x)=sin(2x-
)图象向左平移t(t>0)个单位后,所得图象为f(x+t)=sin[2(x+t)-
]=sin(2x+2t-
),
要使f(x+t)是偶函数,则2t-
=kπ+
,即t=
+
,∵t>0,
∴t的最小值为
.
f(x)=sin(2x-
)图象向右平移s(s>0)个单位后,所得图象为f(x-s)=sin[2(x-s)-
]=sin(2x-2s-
),
要使f(x-s)是奇函数,则2s+
=kπ,即s=
-
,
∵s>0,
∴s的最小值为
,
则.s+t的最小值为
+
=
.
| m |
| n |
| m |
| n |
∴(2a+c)cosB+bcosC=0,
即2acosB+ccosB+bcosC=0,
由正弦定理得2sinAcosB+sinCcosB+cosCsinB=0,
即2sinAcosB+sin(C+B)=0,
∴sinA(2cosB+1)=0,
在三角形中,2cosB+1=0,即cosB=-
| 1 |
| 2 |
| 2π |
| 3 |
(2)∵B=
| 2π |
| 3 |
| π |
| 3 |
f(x)=
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
当x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
-
| ||
| 2 |
| π |
| 3 |
要使f(x)+λ≥0恒成立,
即f(x)≥-λ,
则-λ≥-
| ||
| 2 |
即λ≤
| ||
| 2 |
| ||
| 2 |
(3)将f(x)=sin(2x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
要使f(x+t)是偶函数,则2t-
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| 5π |
| 12 |
∴t的最小值为
| 5π |
| 12 |
f(x)=sin(2x-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
要使f(x-s)是奇函数,则2s+
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
∵s>0,
∴s的最小值为
| π |
| 3 |
则.s+t的最小值为
| 5π |
| 12 |
| π |
| 3 |
| 3π |
| 4 |
点评:本题主要考查三角函数的图象和性质,综合考查三角函数的诱导公式以及辅助角公式的应用,综合性较强,运算量较大.

练习册系列答案
相关题目
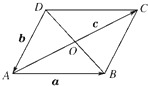 如图所示,O是平行四边形ABCD的对角线AC,BD的交点,设
如图所示,O是平行四边形ABCD的对角线AC,BD的交点,设 如图,在圆锥PO中,已知PO=
如图,在圆锥PO中,已知PO=