题目内容
做投掷2颗骰子的试验,用(x,y)表示结果,其中x表示第1颗骰子出现的点数,y表示第2颗骰子出现的点数,写出:
(1)求事件“出现点数相等”的概率
(2)求事件“出现点数之和大于8”的概率.
(1)求事件“出现点数相等”的概率
(2)求事件“出现点数之和大于8”的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)计算出所有基本事件个数,和满足条件“出现点数相等”的基本事件个数,代入古典概型概率计算公式,可得答案.
(2)计算出所有基本事件个数,和满足条件“出现点数之和大于8”的基本事件个数,代入古典概型概率计算公式,可得答案.
(2)计算出所有基本事件个数,和满足条件“出现点数之和大于8”的基本事件个数,代入古典概型概率计算公式,可得答案.
解答:
解:这个试验的基本事件空间为Ω={(x,y)|1≤x≤6.1≤y,且x∈N,y∈N },
共有36个基本事件. …2
(1)事件“出现点数相同”含有的基本是:
(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)
共有6个基本事件,所以概率为
=
…7
(2)事件“出现点数之和大于8”含有基本事件:
(3,6),(4,5),(5,4),(6,3),(4,6),
(5,5),(6,4),(5,6),(6,5),(6,6),
共有10个基本事件,概率为
=
…12
共有36个基本事件. …2
(1)事件“出现点数相同”含有的基本是:
(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)
共有6个基本事件,所以概率为
| 6 |
| 36 |
| 1 |
| 6 |
(2)事件“出现点数之和大于8”含有基本事件:
(3,6),(4,5),(5,4),(6,3),(4,6),
(5,5),(6,4),(5,6),(6,5),(6,6),
共有10个基本事件,概率为
| 10 |
| 36 |
| 5 |
| 18 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
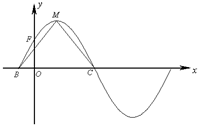 函数f(x)=2sin(ωx+φ)
函数f(x)=2sin(ωx+φ)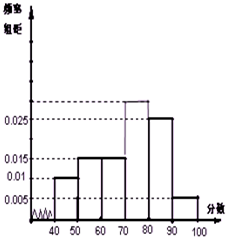 某校从参加高一年级期末考试的学生中抽出60名学生,将其某科成绩(是不小于40不大于100的整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其某科成绩(是不小于40不大于100的整数)分成六段[40,50),[50,60)…[90,100]后画出如下频率分布直方图,根据图形中所给的信息,回答以下问题: