题目内容
销售甲、乙两种商品所得利润分别是P(万元)和Q(万元),它们与投入资金t(万元)的关系有经验公式P=
t,Q=
,今将4万元资金投入经营甲、乙两种商品.其中对乙种商品投资x (万元).
(Ⅰ)试建立总利润y (万元)关于x的函数表达式,并指出定义域;
(Ⅱ)应怎样分配这4万元资金,才能获得最大总利润?并求出最大总利润.
| 1 |
| 5 |
| 2 |
| 5 |
| t |
(Ⅰ)试建立总利润y (万元)关于x的函数表达式,并指出定义域;
(Ⅱ)应怎样分配这4万元资金,才能获得最大总利润?并求出最大总利润.
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(1)当自变量取x时,P函数中的t值为,Q函数的t值应为4-x,分别求得P和Q的值,从而得出当自变量取x时,总利润y万元关于x的函数表达式;
(2)利用换元法转化成一个二次函数的形式,最后结合二次函数的最值求法得出函数的最大值,从而解决问题.
(2)利用换元法转化成一个二次函数的形式,最后结合二次函数的最值求法得出函数的最大值,从而解决问题.
解答:
解:(1)因为对乙种商品投资x万元,所以对甲种商品投资为4-x万元
由题意知:y=P+Q=
(4-x)+
(0≤x≤4)
即y=-
x+
+
(0≤x≤4)…(6分)
(Ⅱ)设
=m,则x=m2,且0≤m≤2.
∴y=-
x+
+
=-
(m2-2m-4)=-
(m-1)2+1
所以当m=1即
=1,也就是x=1万元时,总利润最大,ymax=1万元…(13分)
答:对乙种商品投资1万元,对甲种商品投资3万元,才能获得最大总利润,并且最大总利润为1(万元).…(14分)
由题意知:y=P+Q=
| 1 |
| 5 |
| 2 |
| 5 |
| x |
即y=-
| 1 |
| 5 |
| 2 |
| 5 |
| x |
| 4 |
| 5 |
(Ⅱ)设
| x |
∴y=-
| 1 |
| 5 |
| 2 |
| 5 |
| x |
| 4 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
所以当m=1即
| x |
答:对乙种商品投资1万元,对甲种商品投资3万元,才能获得最大总利润,并且最大总利润为1(万元).…(14分)
点评:本题考查函数模型的选择与应用,通过对实际问题的分析,构造数学模型从而解决问题.需要对知识熟练的掌握并应用,属于中档题.

练习册系列答案
相关题目
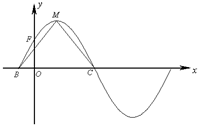 函数f(x)=2sin(ωx+φ)
函数f(x)=2sin(ωx+φ)