题目内容
已知两个单位向量
,
的夹角为60°,
=(1-t)
+t
,若
•
=0,则t= .
| a |
| b |
| c |
| a |
| b |
| b |
| c |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:对
=(1-t)
+t
两边与
作数量积即可得出.
| c |
| a |
| b |
| c |
解答:
解:∵两个单位向量
,
的夹角为60°,
∴
•
=1×1×cos60°=
.
∵
=(1-t)
+t
,
•
=0,
∴0=
•
=(1-t)
•
+t
2,
∴0=
(1-t)+t,解得t=-1,
故答案为:-1.
| a |
| b |
∴
| a |
| b |
| 1 |
| 2 |
∵
| c |
| a |
| b |
| b |
| c |
∴0=
| b |
| c |
| a |
| b |
| b |
∴0=
| 1 |
| 2 |
故答案为:-1.
点评:本题查克拉数量积运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
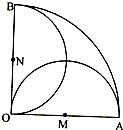 如图,在圆心角为直角的扇形OAB区域中,M、N分别为OA、OB的中点,在M、N两点处各有一个通信基站,其信号的覆盖范围分别为以OA、OB为直径的圆,在扇形OAB内随机取一点,则此点无信号的概率是( )
如图,在圆心角为直角的扇形OAB区域中,M、N分别为OA、OB的中点,在M、N两点处各有一个通信基站,其信号的覆盖范围分别为以OA、OB为直径的圆,在扇形OAB内随机取一点,则此点无信号的概率是( )A、1-
| ||||
B、
| ||||
C、
| ||||
D、
|
若对任意的x>1,
≥a恒成立,则a的最大值是( )
| x2+3 |
| x-1 |
| A、4 | B、6 | C、8 | D、10 |
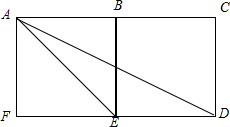 如图所示,四边形ABEF和BCDE均是边长为1的正方形,在以A、B、C、D、E、F为起点和终点的向量中.
如图所示,四边形ABEF和BCDE均是边长为1的正方形,在以A、B、C、D、E、F为起点和终点的向量中.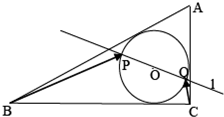 如图,圆O为Rt△ABC的内切圆,已AC=3,BC=4,AB=5,过圆心O的直线l交圆O于P、Q两点,则
如图,圆O为Rt△ABC的内切圆,已AC=3,BC=4,AB=5,过圆心O的直线l交圆O于P、Q两点,则