题目内容
已知向量
和向量
的夹角为135°，|
|=2，|
|=3，则
•
= ．
| a |
| b |
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用数量积的定义即可得出．
解答：
解：∵向量
和向量
的夹角为135°，|
|=2，|
|=3，
则
•
=|
||
|cos135°=2×3×(-
)=-3
．
故答案为：-3
．
| a |
| b |
| a |
| b |
则
| a |
| b |
| a |
| b |
| ||
| 2 |
| 2 |
故答案为：-3
| 2 |
点评：本题考查了数量积对于及其运算性质，考查了计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
（已知集合A={x||x+1|＜1}，B{x|y=
}，则A∩B=（ ）
| 1 | ||
|
| A、（-2，-1） |
| B、（-2，-1] |
| C、（-1，0） |
| D、[-1，0） |
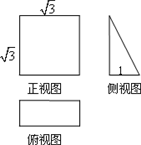一个空间几何体的三视图及部分数据如图所示，则这个几何体的体积为（ ）A、
| ||
| B、1 | ||
C、
| ||
| D、3 |
某组合体的三视图如图所示，其中俯视图的扇形中心角为60°，则该几何体的体积为（ ）
A、
| ||||
B、
| ||||
C、3
| ||||
D、3
|
已知△ABC是边长为2的正三角形，则
•
的值为（ ）
| AB |
| BC |
| A、2 | ||
| B、-2 | ||
C、2
| ||
D、-2
|