题目内容
12.已知平面向量$\overrightarrow a=({3,6}),\overrightarrow b=({x,-1})$,如果$\overrightarrow a∥\overrightarrow b$,那么$|\overrightarrow b|$=( )| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | 3 | D. | $\frac{3}{2}$ |
分析 根据平行向量的坐标关系便可求出x=$-\frac{1}{2}$,从而得出$\overrightarrow{b}=(-\frac{1}{2},-1)$,这便可得出$|\overrightarrow{b}|$的值.
解答 解:∵$\overrightarrow{a}$$∥\overrightarrow{b}$;
∴3•(-1)-6x=0;
∴$x=-\frac{1}{2}$;
∴$\overrightarrow{b}=(-\frac{1}{2},-1)$;
∴$|\overrightarrow{b}|=\sqrt{\frac{1}{4}+1}=\frac{\sqrt{5}}{2}$.
故选B.
点评 考查平行向量的坐标关系,以及根据向量的坐标求向量长度的计算公式.

练习册系列答案
相关题目
3.以点C(-4,3)为圆心的圆与直线2x+y-5=0相离,则圆C的半径R取值范围是( )
| A. | (0,2) | B. | (0,$\sqrt{5}$) | C. | (0,2$\sqrt{5}$) | D. | (0,10) |
17.三角形的一个内角为60°是这个三角形三内角成等差数列的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
2.曲线y=$\frac{1}{2}$x2-2x在x=3处的切线的倾斜角为( )
| A. | 45° | B. | -45° | C. | 135° | D. | -135° |
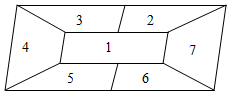 巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种.
巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种.