题目内容
2.已知x,y满足约束条件$\left\{\begin{array}{l}{x-y≤0}\\{x+y≥4}\\{y≤4}\end{array}\right.$,则z=2x+3y的最大值为20.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:由约束条件$\left\{\begin{array}{l}{x-y≤0}\\{x+y≥4}\\{y≤4}\end{array}\right.$作出可行域如图,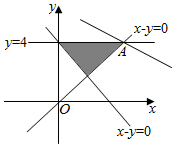
联立$\left\{\begin{array}{l}{y=4}\\{x-y=0}\end{array}\right.$,解得A(4,4),
化目标函数z=2x+3y为$y=-\frac{2}{3}x+\frac{z}{3}$,
由图可知,当直线$y=-\frac{2}{3}x+\frac{z}{3}$过A时,直线在y轴上的截距最大,
z有最大值为20.
故答案为:20.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
12.已知全集U=R,集合A={x|x<-1或x>4),B={x|-2≤x≤3),那么阴影部分表示的集合为( )
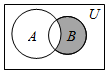

| A. | {x|-2≤x<4} | B. | {x|x≤3或x≥4} | C. | {x|-2≤x≤一1} | D. | {x|-1≤x≤3} |
10.若双曲线的顶点和焦点分别为椭圆$\frac{{x}^{2}}{2}$+y2=1的焦点和顶点,则该双曲线方程为( )
| A. | x2-y2=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | C. | x2-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 |
14.若f(x)=xex-a有两个零点,则实数a的取值范围是( )
| A. | ($\frac{1}{e}$,+∞) | B. | (0,$\frac{1}{e}$) | C. | (-$\frac{1}{e}$,+∞) | D. | (-$\frac{1}{e}$,0) |
12.已知平面向量$\overrightarrow a=({3,6}),\overrightarrow b=({x,-1})$,如果$\overrightarrow a∥\overrightarrow b$,那么$|\overrightarrow b|$=( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | 3 | D. | $\frac{3}{2}$ |
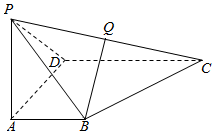 如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.
如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD,Q是PC的中点.