题目内容
5.已知点A(-4,-3),B(2,9),圆C是以线段AB为直径的圆.(1)求圆C的方程;
(2)设点P(0,2)则求圆内以P为中点的弦所在的直线l0的方程.
分析 (1)求出圆的圆心与半径,即可求圆C的方程;
(2)求出所求直线的斜率,然后求解以点P为中点的弦所在的直线方程.
解答 解:(1)AB的中点坐标为C(-1,3),半径为$\sqrt{(-4+1)^{2}+(-3-3)^{2}}$=$\sqrt{45}$,
∴圆C的方程为(x+1)2+(y-3)2=45;
(2)kCP=$\frac{3-2}{-1-0}$=-1,
∴以点P为中点的弦所在的直线的斜率为:1.
以点P为中点的弦所在的直线方程为:y-2=x-0.
即x-y+2=0.
点评 本题考查直线与圆的位置关系,直线方程的求法,考查计算能力.

练习册系列答案
相关题目
16.世园会期间,某班有四名学生参加了志愿工作.将这四名学生分配到A,B,C三个不同的展馆服务,每个展馆至少分配一人.则四人中学生甲不到A馆的概率为( )
| A. | 1 | B. | $\frac{5}{6}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
13.已知集合A={y|y=$\sqrt{2-x}$},B={x|x2-2x>0},则( )
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
15.已知角α的终边经过点P(-1,1),则cosα的值为( )
| A. | 1 | B. | -1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
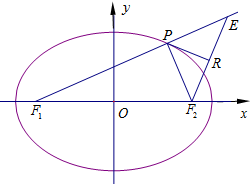 已知F1,F2分别为椭圆的左、右两个焦点,椭圆的离心率为$\frac{\sqrt{6}}{3}$,短轴的一个端点到一个焦点的距离为$\sqrt{3}$.设点P是椭圆上的动点,过点F2作∠F1PF2的外角平分线PR的垂线,交F1P的延长线于E,垂足为R.
已知F1,F2分别为椭圆的左、右两个焦点,椭圆的离心率为$\frac{\sqrt{6}}{3}$,短轴的一个端点到一个焦点的距离为$\sqrt{3}$.设点P是椭圆上的动点,过点F2作∠F1PF2的外角平分线PR的垂线,交F1P的延长线于E,垂足为R.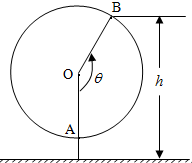 如图为一个观览车示意图.该观览车圆半径为5米,圆上最低点与地面距离为1米,60秒转动一圈.图中OA与地面垂直.设从OA开始转动,逆时针转动θ角到OB.设B点与地面距离为h.
如图为一个观览车示意图.该观览车圆半径为5米,圆上最低点与地面距离为1米,60秒转动一圈.图中OA与地面垂直.设从OA开始转动,逆时针转动θ角到OB.设B点与地面距离为h.