Question

15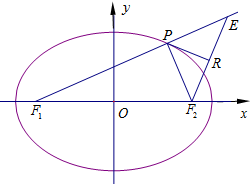．已知F₁，F₂分别为椭圆的左、右两个焦点，椭圆的离心率为$\frac{\sqrt{6}}{3}$，短轴的一个端点到一个焦点的距离为$\sqrt{3}$．设点P是椭圆上的动点，过点F₂作∠F₁PF₂的外角平分线PR的垂线，交F₁P的延长线于E，垂足为R．
（1）求椭圆的标准方程；
（2）求点R的轨迹方程；
（3）求证：$\overrightarrow{R{F_1}}•\overrightarrow{R{F_2}}$为定值．

Answer 1

分析 （1）设椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0），由题意可得：a=$\sqrt{3}$，$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$，a²=b²+c²，联立解出即可得出．
（2）利用线段的垂直平分线的性质、中点坐标公式即可得出．
（3）利用数量积运算性质即可证明．

解答 解：（1）设椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0），
则$\left\{\begin{array}{l}a=\sqrt{3}\\ \frac{c}{a}=\frac{{\sqrt{6}}}{3}\\{a^2}={b^2}+{c^2}\end{array}\right.$$⇒\left\{\begin{array}{l}a=\sqrt{3}\\ b=1\end{array}\right.$，
椭圆的方程为$\frac{x^2}{3}+{y^2}=1$．
（2）设F₂R交F₁P于Q，由题意知直线m垂直平分线段F₂E．
得到PF₂=PE，又O为F₁F₂中点，R为F₂E的中点，
∴$OR=\frac{1}{2}{F_1}E=\frac{1}{2}（{F_1}P+PE）=\frac{1}{2}（{F_1}P+P{F_2}）=\frac{1}{2}•2a=a=\sqrt{3}$．
因此所求R点轨迹方程为x²+y²=3（y≠0）．
（3）证明：设R（x，y），
则$\overrightarrow{R{F_1}}=（-\sqrt{2}-x，0-y），\overrightarrow{R{F_2}}=（\sqrt{2}-x，0-y）$，
∴$\overrightarrow{R{F_1}}•\overrightarrow{R{F_2}}=-（2-{x^2}）+{y^2}={x^2}+{y^2}=1$．

点评 本题考查了椭圆与圆的定义标准方程及其性质、直线与椭圆相交问题、数量积运算性质、中点坐标公式、线段的垂直平分线的性质，考查了推理能力与计算能力，属于中档题．