题目内容
14.已知直线l:x-y-4=0和圆C:x2+y2+2x-2y=0(1)试判断直线l与圆C的位置关系
(2)求与直线l和圆C都相切的半径最小的圆的方程.
分析 (1)求出圆心到直线的距离与半径比较,即可得出结论;
(2)由题意过圆心(-1,1)与直线x-y-4=0垂直的直线方程为x+y=0,所求的圆的圆心在此直线上,所求的圆的半径为$\sqrt{2}$,即可求出所求圆的方程.
解答 解:(1)圆C:x2+y2+2x-2y=0,可化为(x+1)2+(y-1)2=2,
∴圆x2+y2+2x-2y=0的圆心为(-1,1),半径为$\sqrt{2}$,
圆心到直线的距离d=$\frac{|-1-1-4|}{\sqrt{2}}$=3$\sqrt{2}$>$\sqrt{2}$,
∴直线l与圆C相离;
(2)由题意,过圆心(-1,1)与直线x-y-4=0垂直的直线方程为x+y=0,
所求的圆的圆心在此直线上,
又圆心(-1,1)到直线x-y-4=0的距离为d=$\frac{|-1-1-4|}{\sqrt{2}}$=3$\sqrt{2}$,
则所求的圆的半径为$\sqrt{2}$,
设所求圆心坐标为(a,b)
则$\frac{|a-b-4|}{\sqrt{2}}$=$\sqrt{2}$,且a+b=0
解得a=1,b=-1,
∴与直线l和圆C都相切的半径最小的圆的方程为(x-1)2+(y+1)2=2
点评 本题是中档题,考查直线与圆的位置关系,数形结合的思想,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若函数y=f(x)是定义在R上的奇函数,且在区间(-∞,0]上是减函数,则不等式f(lnx)<-f(1)的解集为( )
| A. | (e,+∞) | B. | (${\frac{1}{e}$,+∞) | C. | (${\frac{1}{e}$,e) | D. | (0,$\frac{1}{e}$) |
19.调查200名50岁以上有吸烟习惯与患慢性气管炎的人的情况,获数据如表
(1)表中s,t的值分别是多少;
(2)试问:有吸烟习惯与患慢性气管炎病是否有关?
| 患慢性气管炎 | 未患慢性气管炎 | 总计 | |
| 吸烟 | s | 30 | 100 |
| 不吸烟 | 35 | t | 100 |
| 合计 | 105 | 95 | 200 |
(2)试问:有吸烟习惯与患慢性气管炎病是否有关?
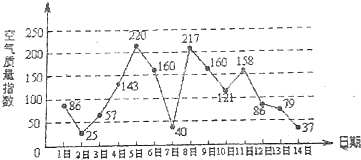 如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.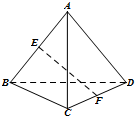 如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )
如图,在空间四边形ABCD中,AD=2$\sqrt{2}$,BC=2,E,F分别是AB,CD的中点,若EF=$\sqrt{3}$,则异面直线AD与BC所成角的大小为( )