题目内容

设P是圆x2+（y-2）2=1上的一个动点，Q为双曲线x2-y2=1上一动点，则PQ的最小值是（　　）
A、
3
B、
5
C、
5
-2
D、
3
-1
考点：双曲线的简单性质
专题：圆锥曲线中的最值与范围问题
分析：设Q（x，y）为双曲线x2-y2=1上一动点，圆x2+（y-2）2=1的圆心C（0，2），可得CQ|=
x2+(y-2)2
=
2(y-1)2+3
≥
3
，因此|PQ|的最小值是
3
-r．
解答： 解：设Q（x，y）为双曲线x2-y2=1上一动点，圆x2+（y-2）2=1的圆心C（0，2），
则CQ|=
x2+(y-2)2
=
2(y-1)2+3
≥
3
，
∴|PQ|的最小值是
3
-1．
故选：D．
点评：本题考查了两点之间的距离公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
计算下列各题的值．
（1）已知函数f（x）=ax+a-x（a＞0，a≠1），且f（1）=3，计算f（0）+f（1）+f（2）的值；
（2）设2a=5b=m，且
1
a
+
1
b
=1，求m的值．
已知圆C：（x-1）2+（y-2）2=16，直线l：（2m+1）x+（m+1）y-7m-4=0（m∈R）
（Ⅰ）证明直线l恒过定点；
（Ⅱ）判断直线l与圆C的位置关系；
（Ⅲ）当点M（x，y）在圆C上运动时，求
y
x+3
的取值范围．
设F是椭圆E：
x2
a2
+
y2
b2
=1，（a＞b＞0）的左焦点，直线l方程为x=-
a2
c
（其中a为椭圆的长半轴长，c为半焦距），设直线l与x轴交于P点，MN为椭圆E的长轴，已知|MN|=8，且|PM|=2|MF|．
（1）求椭圆E的标准方程；
（2）过点P作直线m与椭圆E交于A，B两点，求证：∠AFM=∠BFN；
（3）在（2）的条件下，求三角形△ABF面积的最大值及此时直线m的方程．
在直角坐标系xOy中，已知点A（1，1），B（2，3），C（3，2），点P（x，y）在△ABC三边围城的区域（含边界）上．
（1）若
AP
⊥
BC
，
CP
⊥
AB
，求|
OP
|；
（2）设
OP
=m
AB
+n
AC
（m，n∈R）用x，y表示m+n，并求m+n的最小值．
下列命题正确的是（　　）
A、若向量
a
与向量
b
的方向相反，则称向量
a
为向量
b
的相反向量
B、若向量
a
与向量
b
的模相等，则称向量
a
与向量
b
为相等向量
C、若向量
a
的模等于0，则向量
a
等于0
D、若向量
a
是单位向量，则向量
a
的模等于1
广东某六所名校联盟办学，他们不但注重学生的学习成绩的提高，更重视学生的综合素质的提高；六校从各校中抽出部分学生组成甲、乙、丙、丁 4个小组进行综合素质过关测试，设4个小组中：甲、乙、丙、丁组在测试中能够过关的概率分别为0.6，0.5，0.5，0.4，各组是否过关是相互独立的．
（1）求测试中至少3个小组过关的概率；
（2）X表示测试中能够过关的组数，求X的数学期望．
已知在△ABC中，三条边a，b、c所对的角分别为A、B，C，向量
m
=（sinA，cosA），
n
=（cosB，sinB），且满足
m
•
n
=sin2C．
（1）求角C的大小；
（2）若sinA，sinC，sinB成等比数列，且
AC
•（
AB
-
AC
）=-8，求边c的值并求△ABC外接圆的面积．
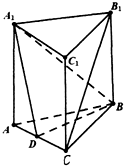在直三棱柱中，AA1=AB=BC=3，AC=2，D是AC中点．
（1）求证：B1C∥平面A1BD；
（2）求点B1到平面A1BD的距离；
（3）求二面角A1-DB-B1的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网