题目内容
t为何值时，函数f（ x）=-3x2+2x-t+1的图象与x轴不相交．
考点：二次函数的性质
专题：函数的性质及应用
分析：函数f（ x）=-3x2+2x-t+1的图象与x轴不相交等价于对应二次方程的△＜0，求解即可．
解答：
解；函数f（ x）=-3x2+2x-t+1为二次函数，其图象与x轴不相交，
则二次方程-3x2+2x-t+1=0无实数解，
∴△＜0，即4-4×（-3）×（-t+1）＜0，
解得t＞
．
则二次方程-3x2+2x-t+1=0无实数解，
∴△＜0，即4-4×（-3）×（-t+1）＜0，
解得t＞
| 4 |
| 3 |
点评：本题考查二次函数图象与性质，与x轴交点个数可以等价与对应方程的判别式符号．
练习册系列答案
相关题目
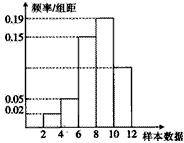有一个容量为200的样本，其频率分布直方图如图所示，根据样本的频率分布直方图估计，样本数据落在[10，12）内的频数为若从5名男歌手和4名女歌手中各选一人参加“星光大道”节目，则不同的选法种数是（ ）
| A、5种 | B、4种 | C、9种 | D、20种 |