题目内容
已知方程x3-
x2+6x-a=0有且只有一个实数根，求实数a的取值范围．
| 2 |
| 9 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：将问题转化为f（x）=F（x）-a=0有且仅有一个实数根时，则表示直线y=a与F（x）仅有一个交点，通过求导得到F（x）的图象，从而得到答案．
解答：
解：设F（x）=x3-
x2+6x，
∴F（x）'=3x2-9x+6=3（x2-3x+2）=3（x-1）（x-2），
令F（x）＞0，解得：x＞2或x＜1，令F（x）＜0，解得：1＜x＜2，
即F（x）在（-∞，1）为增函数，F（x）极大=F（1）=
，
F（x）在（1，2）为减函数，F（x）极小=F（2）=2，
F（x）在（2，+∞）为增函数，x→+∞，F（x）→+∞，
f（x）=F（x）-a=0有且仅有一个实数根时，则表示直线y=a与F（x）仅有一个交点，
画出函数F（x）的图象，如图示：
∴当a＞
或a＜2时，F（x）-a=0有且仅有一个实数根．
| 9 |
| 2 |
∴F（x）'=3x2-9x+6=3（x2-3x+2）=3（x-1）（x-2），
令F（x）＞0，解得：x＞2或x＜1，令F（x）＜0，解得：1＜x＜2，
即F（x）在（-∞，1）为增函数，F（x）极大=F（1）=
| 5 |
| 2 |
F（x）在（1，2）为减函数，F（x）极小=F（2）=2，
F（x）在（2，+∞）为增函数，x→+∞，F（x）→+∞，
f（x）=F（x）-a=0有且仅有一个实数根时，则表示直线y=a与F（x）仅有一个交点，
画出函数F（x）的图象，如图示：
∴当a＞
| 5 |
| 2 |
点评：本题考查了根的存在性问题，考查了转化思想，考查了函数的极值问题，是一道中档题．
练习册系列答案
相关题目
设函数f（x）=
，若f（a）=8，则a=（ ）
|
| A、-8或-2 | B、-2或2 |
| C、-8或2 | D、-2或8 |
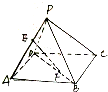如图，P是?ABCD所在平面外一点，E、F分别在PA、BD上，且PE：EA=BF：FD，求证：EF∥平面PBC．
