题目内容
20.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F2,过F2作其中一条渐近线的垂线,分别交y轴和该渐近线于M,N两点,且$\overrightarrow{MN}$=3$\overrightarrow{N{F}_{2}}$,则$\frac{a}{b}$=$\sqrt{3}$.分析 设渐近线的方程为y=$\frac{b}{a}$x,过N作x轴的垂线,垂足为P,根据向量关系建立长度关系进行求解即可.
解答 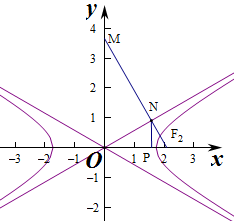 解:设渐近线的方程为y=$\frac{b}{a}$x,过N作x轴的垂线,垂足为P,
解:设渐近线的方程为y=$\frac{b}{a}$x,过N作x轴的垂线,垂足为P,
由$\overrightarrow{MN}$=3$\overrightarrow{N{F}_{2}}$,得$\frac{|{F}_{2}P|}{|O{F}_{2}|}$=$\frac{|{F}_{2}N|}{|{F}_{2}M|}$=$\frac{1}{4}$,
得N的坐标为($\frac{3c}{4}$,$\frac{3bc}{4a}$),
∵NF2⊥ON,
∴$\frac{3bc}{4a}÷(\frac{3c}{4}-c)$=-$\frac{a}{b}$,
化简得$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{3}$,
则$\frac{a}{b}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$
点评 本题主要考查双曲线向量的计算,根据条件结合向量共线的条件进行转化是解决本题的关键.

练习册系列答案
相关题目
11.若双曲线上存在点P,使得P到两个焦点的距离之比为2:1,则称此双曲线存在“L点”,下列双曲线中存在“L点”的是( )
| A. | ${x^2}-\frac{y^2}{4}=1$ | B. | ${x^2}-\frac{y^2}{9}=1$ | C. | ${x^2}-\frac{y^2}{15}=1$ | D. | ${x^2}-\frac{y^2}{24}=1$ |
8.已知O为原点,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1(a>0)上的点P作两条渐近线的平行线,且与两渐近线的交点分别为A,B,平行四边形OBPA的面积为2,则此双曲线的渐近线方程为( )
| A. | y=±$\frac{1}{4}$x | B. | y=±$\frac{1}{3}$x | C. | y=±$\frac{1}{2}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
15.小芳投掷一枚均匀的骰子,则它投掷得的点数为奇数的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{6}$ |
5.一次函数y=-$\frac{m}{n}$x+$\frac{1}{n}$的图象同时经过第一、二、四象限的必要不充分条件是( )
| A. | mn>0 | B. | m>1,且n>1 | C. | m>0,且n<0 | D. | m>0,且n>0 |
12.sin80°cos70°+sin10°sin70°=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
9.直线$\sqrt{3}$x-y+3=0的倾斜角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 150° |