题目内容

10．设变量x，y满足约束条件$\left\{{\begin{array}{l}{x+2y-4≤0}\\{3x+y-3≥0}\\{x-y-1≤0}\end{array}}\right.$，则目标函数z=x-2y的最小值为（　　）
A．$-\frac{16}{5}$B．-3C．0D．1

分析 画出约束条件的可行域，利用目标函数的几何意义求解最小值即可．

解答 解：画出满足条件的平面区域，如图示：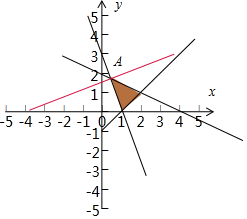

，
由$\left\{\begin{array}{l}{x+2y-4=0}\\{3x+y-3=0}\end{array}\right.$，解得A（$\frac{2}{5}$，$\frac{9}{5}$），
由z=x-2y得：y=$\frac{1}{2}$x-$\frac{1}{2}$z，
平移直线y=$\frac{1}{2}$x，结合图象直线过A（$\frac{2}{5}$，$\frac{9}{5}$）时，z最小，
z的最小值是：-$\frac{16}{5}$，
故选：A．

点评 本题考查了简单的线性规划问题，考查数形结合思想，是一道中档题．

练习册系列答案
相关题目
20．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F2，过F2作其中一条渐近线的垂线，分别交y轴和该渐近线于M，N两点，且$\overrightarrow{MN}$=3$\overrightarrow{N{F}_{2}}$，则$\frac{a}{b}$=$\sqrt{3}$．
1．已知全集U={1，2，3，4，5，6}，集合A={1，2，4}，集合B={3，6}，则∁U（A∪B）=（　　）
A．{1，2，4}B．{1，2，4，5}C．{2，4}D．{5}
18．函数f（x）=$\frac{1}{lo{g}_{2}x}$的大致图象是（　　）
A．B．C．D．
5．已知函数f（x）=$\frac{1}{x-1}$，x∈[2，6]．
（1）证明f（x）是减函数；
（2）若函数g（x）=f（x）+sinα的最大值为0，求α的值．
15．已知f（x）=（x2-3）ex（其中x∈R，e是自然对数的底数），当t1＞0时，关于x的方程[f（x）-t1][f（x）-t2]=0恰好有5个实数根，则实数t2的取值范围是（　　）
A．（-2e，0）B．（-2e，0]C．[-2e，6e-3]D．（-2e，6e-3）
2．已知函数$f（x）=2cosx（{cosx+\sqrt{3}sinx}）+a（{a∈R}）$．
（1）求f（x）的最小正周期；
（2）当$x∈[{0，\frac{π}{2}}]$时，f（x）的最小值为2，求a的值．
19．在等比数列{an}中，已知${a_1}=\frac{1}{4}，{a_3}{a_5}=4（{{a_4}-1}）$，则{an}的前10项和S10=$\frac{1023}{4}$．
20．圆O的半径为定长，A是平面上一定点，P是圆上任意一点，线段AP的垂直平分线l和直线OP相交于点Q，当点P在圆上运动时，点Q的轨迹为（　　）
A．一个点B．椭圆
C．双曲线D．以上选项都有可能

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网