题目内容
18.已知锐角α,β满足$\frac{sinα}{cosβ}$+$\frac{sinβ}{cosα}$<2,设f(x)=logax(0<a<1),则下列判断正确的是( )| A. | f(sinα)>f(cosβ) | B. | f(cosα)>f(sinβ) | C. | f(sinα)<f(sinβ) | D. | f(cosα)<f(cosβ) |
分析 由题意可得锐角α,β满足$α+β<\frac{π}{2}$,由此求得sinα<cosβ,再由复合函数的单调性得答案.
解答 解:∵锐角α,β满足α+β$>\frac{π}{2}$,则$α>\frac{π}{2}-β$,sinα>sin($\frac{π}{2}-β$)=cosβ,∴$\frac{sinα}{cosβ}>1$,
同理$\frac{sinβ}{cosα}$>1,则$\frac{sinα}{cosβ}$+$\frac{sinβ}{cosα}$>2,与已知矛盾;
∴$α+β<\frac{π}{2}$.
即$α<\frac{π}{2}-β$,∴$sinα<sin(\frac{π}{2}-β)=cosβ$,
∵f(x)=logax(0<a<1)为减函数,
∴f(sinα)>f(cosβ).
故选:A.
点评 本题考查三角函数的单调性,考查三角函数值的大小比较,训练了复合函数单调性的判定方法,是中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
9.已知两点A(1,2),B(4,-2),则与向量$\overrightarrow{AB}$共线的单位向量$\overrightarrow{e}$是( )
| A. | (3,-4) | B. | (3,-4),(-3,4) | C. | ($\frac{3}{5}$,一$\frac{4}{5}$) | D. | ($\frac{3}{5}$,一$\frac{4}{5}$),(一$\frac{3}{5}$,$\frac{4}{5}$) |
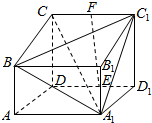 如图,四棱柱ABCD-A1B1C1D1中,侧面AA1D1D为矩形,AB⊥平面AA1D1D,CD⊥平面AA1D1D,E、F分别为A1B1、CC1的中点,且AA1=CD=2,AB=AD=1.
如图,四棱柱ABCD-A1B1C1D1中,侧面AA1D1D为矩形,AB⊥平面AA1D1D,CD⊥平面AA1D1D,E、F分别为A1B1、CC1的中点,且AA1=CD=2,AB=AD=1.