题目内容
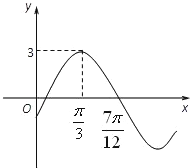 已知函数f(x)=Asin(ωx+ϕ),(其中x∈R,A>0,ω>0,|ϕ|<
已知函数f(x)=Asin(ωx+ϕ),(其中x∈R,A>0,ω>0,|ϕ|<| π |
| 2 |
(1)求f(x)的解析式;
(2)当x∈[
| π |
| 6 |
| 2π |
| 3 |
(3)把函数y=f(x)图象向左平移
| π |
| 3 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)根据三角函数的图象即可确定f(x)的解析式;
(2)根据三角函数的性质即可求f(x)的最大值及f(x)取最大值时x的集合;
(3)根据三角函数的函数关系求出g(x),利用三角函数的图象和性质即可得到结论.
(2)根据三角函数的性质即可求f(x)的最大值及f(x)取最大值时x的集合;
(3)根据三角函数的函数关系求出g(x),利用三角函数的图象和性质即可得到结论.
解答:
解:(1)函数周期T=4×(
-
)=π=
,
则ω=2,
由图象可知A=3,
则f(x)=3sin(2x+φ),
当x=
时,2×
+φ=
,
解得φ=-
,
则f(x)的解析式为f(x)=3sin(2x-
);
(2)当x∈[
,
]时,当2x-
∈[-
,
]时
当2x-
=
,即x=
时,sin(
x+
)=1,
此时函数f(x)的取得最大值3.
(3)把函数y=f(x)图象向左平移
个单位,得到函数y=3sin[2(x+
)-
]=3sin(2x+
)=3cos2x;
即y=g(x)=3cos2x,
由2x=2kπ+
,解得x=kπ+
,即g(x)图象的对称中心为(kπ+
,0).
由2x=2kπ,k∈Z,解得x=kπ,
即g(x)图象的对称轴为x=kπ,k∈Z
| 7π |
| 12 |
| π |
| 3 |
| 2π |
| ω |
则ω=2,
由图象可知A=3,
则f(x)=3sin(2x+φ),
当x=
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
解得φ=-
| π |
| 6 |
则f(x)的解析式为f(x)=3sin(2x-
| π |
| 6 |
(2)当x∈[
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
当2x-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
此时函数f(x)的取得最大值3.
(3)把函数y=f(x)图象向左平移
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
即y=g(x)=3cos2x,
由2x=2kπ+
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
由2x=2kπ,k∈Z,解得x=kπ,
即g(x)图象的对称轴为x=kπ,k∈Z
点评:本题主要考查三角函数的解析式的求解以及三角函数性质是综合应用,根据条件确定函数的解析式是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
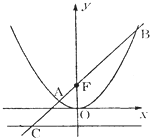 如图,过抛物线x2=2py (p>0)焦点F的直线l交抛物线于点A、B,交准线于点C,若|AC|=2|AF|,且|BF|=8,则此抛物线的方程为( )
如图,过抛物线x2=2py (p>0)焦点F的直线l交抛物线于点A、B,交准线于点C,若|AC|=2|AF|,且|BF|=8,则此抛物线的方程为( )| A、x2=4y |
| B、x2=8 y |
| C、x2=2y |
| D、x2=16y |
小明参加“欧洲六国游”旅行,其中A、B、C三国游览的先后顺序一定(游A、B、C三国的顺序可以相邻也可以不相邻)则小明“欧洲六国游”旅行共有( )种不同的出游方法.
| A、120 | B、180 |
| C、240 | D、480 |
