题目内容
在一个二面角的两个面内部和二面角的棱垂直的两个向量分别为(0,-1,3),(2,2,4),则这个二面角的度数是 .
考点:用空间向量求平面间的夹角
专题:空间角
分析:由空间向量的坐标运算,求出数量积和模,运用向量的夹角公式,即可求出二面角的平面角的余弦值.
解答:
解:设
=(0,-1,3),
=(2,2,4),则
•
=0-2+12=10,|
|=
,|
|=2
,
故这个二面角的余弦值为:cosθ=
=
=
,
则这个二面角的度数是:arccos
.
故答案为:arccos
.
| m |
| n |
| m |
| n |
| m |
| 10 |
| n |
| 6 |
故这个二面角的余弦值为:cosθ=
| ||||
|
|
| 10 | ||||
|
| ||
| 6 |
则这个二面角的度数是:arccos
| ||
| 6 |
故答案为:arccos
| ||
| 6 |
点评:本题考查空间向量求解二面角的平面角,考查计算能力.

练习册系列答案
相关题目
直线L与双曲线
-
=1相交于A,B两点,点N满足
=
,且点N的坐标是(-12,-15),则直线L必过双曲线的( )
| x2 |
| 4 |
| y2 |
| 5 |
| AN |
| NB |
| A、左顶点 | B、右顶点 |
| C、左焦点 | D、右焦点 |
当a取不同的实数时,由方程x2+y2+2ax+2ay-1=0可以得到不同的圆,则( )
| A、这些圆的圆心都在直线y=x上 |
| B、这些圆的圆心都在直线y=-x上 |
| C、这些圆的圆心都在直线y=x或直线y=-x上 |
| D、这些圆的圆心不在同一直线上 |
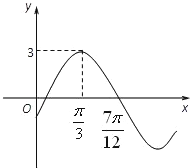 已知函数f(x)=Asin(ωx+ϕ),(其中x∈R,A>0,ω>0,|ϕ|<
已知函数f(x)=Asin(ωx+ϕ),(其中x∈R,A>0,ω>0,|ϕ|<