题目内容

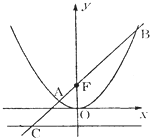如图，过抛物线x2=2py （p＞0）焦点F的直线l交抛物线于点A、B，交准线于点C，若|AC|=2|AF|，且|BF|=8，则此抛物线的方程为（　　）
A、x2=4y
B、x2=8 y
C、x2=2y
D、x2=16y
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由题意求得直线AB的斜率，写出直线方程的点斜式，和抛物线联立后求得B的纵坐标，由抛物线的焦点弦公式结合|BF|=8求得2p，则抛物线方程可求．
解答： 解：如图，

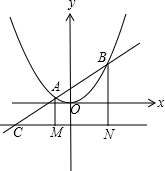
由|AC|=2|AF|，得∠ACM=30°，
即直线l的倾斜角为30°，斜率为
3
3
．
∴AB方程为y=
3
3
x+
p
2
，
联立
y=
3
3
x+
p
2
x2=2py
，得12y2-20py+3p2=0．
解得：y1=
p
6
，y2=
3p
2
．
由图可知：|BF|=|BN|=
3p
2
+
p
2
=2p，
∴2p=8．
则抛物线的方程为x2=8y．
故选：B．
点评：本题考查了抛物线的简单几何性质，考查了抛物线的焦点弦公式，体现了数学转化思想方法，是中档题．
练习册系列答案
相关题目
设全集为R，A={x|x（x-2）＜0}，B={x|y=ln（1-x）}，则A∩（∁RB）=（　　）
A、（-2，1）
B、[1，2）
C、（-2，1]
D、（1，2）
给出以下命题：
①如果函数f（x）在区间（a，b）内可导，那么导数等于零的点一定是极值点；
②若复数z1，z2满足z1+z2，z1•z2都是实数，则z1，z2互为共轭复数；
③连续函数f（x）的图象与直线y=0，x=b（a＜b）所围成的面积是
∫
b
a
f（x）dx；
④反证法就是通过证明逆命题来证明原命题．
其中正确命题的个数是（　　）
A、3B、2C、1D、0
已知|
OA
|=1，|
OB
|=
3
，且
AO
⊥
OB
，设
OC
=m
OA
+n
OB

（1）若C点满足
AC
=t
CB
，求m+n的值；
（2）若C满足∠AOC=30°，求
m
n
的值．
已知点P为抛物线y2=4x上的动点，点P在y轴上的射影是M，点A的坐标是（6，5），则|PA|+|PM|的最小值是（　　）
A、8
B、7
C、5
2
D、5
2
-1
在△ABC中，a、b、c分别是角A、B、C的对边，且（2a+b）cosC+ccosB=0．
（2）求∠C；
（2）若a、b、c成等差数列，b=5，求△ABC的面积．
已知函数f（x）=x2+（a-1）x+a为偶函数．
（1）求a的值；
（2）设函数，g（x）=
f(x)
x
，当x∈[1，+∞]时，不等式g（x）+f（m）+2m≥5恒成立，求m的取值范围．
已知双曲线C：
x2
a2
-
y2
b2
=1的焦点为F（-c，0），F′（c，0），c＞0，过F且平行于双曲线渐近线的直线与抛物线y2=4cx交于点P，若P在以FF′为直径的圆上，则该双曲线的离心率平方为（　　）
A、
3+
5
2
B、
5
C、
5
-1
2
D、
1+
5
2
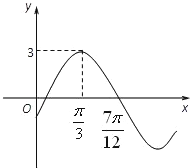已知函数f（x）=Asin（ωx+ϕ），（其中x∈R，A＞0，ω＞0，|ϕ|＜
π
2
）的部分图象如图所示．
（1）求f（x）的解析式；
（2）当x∈[
π
6
，
2π
3
]时，f（x）的最值及其对应x的值；
（3）把函数y=f（x）图象向左平移
π
3
个单位，得到函数y=g（x）图象，请写出g（x）表达式并求出g（x）图象的对称轴和对称中心．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网