题目内容
已知等差数列{an}的前n项和为Sn,S5=3a5=15则数列{
}的前2014项和为 .
| 1 |
| anan+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:依题意可求得等差数列{an}的通项公式an=n,利用裂项法得
=
=
-
,从而可得数列{
}的前2014项和.
| 1 |
| anan+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| anan+1 |
解答:
解:∵数列{an}为等差数列,3a5=15,
∴a5=5;又S5=
=
=15,
∴a3=3;
∴公差d=
=1,
∴an=a3+(n-3)×d=3+(n-3)=n;
∴
=
=
-
,
∴S2014=(1-
)+(
-
)+…+(
-
)=1-
=
.
故答案为:
.
∴a5=5;又S5=
| 5×(a1+a5) |
| 2 |
| 5×2a3 |
| 2 |
∴a3=3;
∴公差d=
| 5-3 |
| 5-3 |
∴an=a3+(n-3)×d=3+(n-3)=n;
∴
| 1 |
| anan+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴S2014=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| 1 |
| 2015 |
| 1 |
| 2015 |
| 2014 |
| 2015 |
故答案为:
| 2014 |
| 2015 |
点评:本题考查数列的求和,着重考查等差数列的通项公式与裂项法求和的综合应用,属于中档题.

练习册系列答案
相关题目
过双曲线2x2-y2-2=0的右焦点作直线l交曲线于A、B两点,若|AB|=4则这样的直线存在( )
| A、0条 | B、1条 | C、2条 | D、3条 |
在△ABC中,A=60°,b=1,S△ABC=
,则
=( )
| 3 |
| a+b+c |
| sinA+sinB+sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
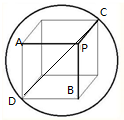 如图,已知球O,球面上有四点P、A、B、C,且PC、PA、PB两两垂直,PC=5,PA=3,PB=4,若过C点的直径为CD,求二面角P-CD-A的大小.
如图,已知球O,球面上有四点P、A、B、C,且PC、PA、PB两两垂直,PC=5,PA=3,PB=4,若过C点的直径为CD,求二面角P-CD-A的大小.