题目内容
已知在△ABC中，重心H的坐标是（5，2），点A的坐标是（-10，2），点B的坐标是（6，4），求点C的坐标．
考点：三角形五心
专题：直线与圆
分析：由题意，设出点C的坐标，根据重心与三个顶点坐标的关系式建立方程组，求出点C的坐标．
解答：
解：设点C（x，y），
由重心坐标公式得
，
解得x=9，y=10；
∴点C的坐标为（9，10）．
由重心坐标公式得
|
解得x=9，y=10；
∴点C的坐标为（9，10）．
点评：本题考查了重心的坐标公式的应用问题，解题的关键是熟记重心与三个顶点的坐标公式，是基础题．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
已知a=sin
，b=cos
，c=1，则a，b，c的大小顺序为（ ）
| 3 |
| 4 |
| 3 |
| 4 |
| A、a＜b＜c |
| B、b＜a＜c |
| C、c＜b＜a |
| D、c＜a＜b |
过双曲线2x2-y2-2=0的右焦点作直线l交曲线于A、B两点，若|AB|=4则这样的直线存在（ ）
| A、0条 | B、1条 | C、2条 | D、3条 |
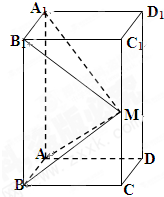如图，在长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，M为CC1的中点在△ABC中，A=60°，b=1，S△ABC=
，则
=（ ）
| 3 |
| a+b+c |
| sinA+sinB+sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|