题目内容
已知
，
是不共线的向量，若A，B，P三点共线，求证：存在实数x，y使
=x
+y
且x+y=1，反之成立．
| OA |
| OB |
| OP |
| OA |
| OB |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：先想着用
，
来表示
，根据向量的加法运算，
=
+
，因为A，B，P三点共线，所以
，
共线，根据共线向量基本定理，存在实数λ使：
=λ
=λ(
-
)．所以能得到
=(1-λ)
+λ
，所以存在实数x=1-λ，y=λ使
=x
+y
且x+y=1，这算正着证完了，再证明反之成立．先根据x+y=1得到：
=(1-y)
+y
=
+y
，再根据向量的加法运算，
=
+
，所以得到：
=y
，所以根据共线向量基本定理得出A，B，P三点共线．
| OA |
| OB |
| OP |
| OP |
| OA |
| AP |
| AP |
| AB |
| AP |
| AB |
| OB |
| OA |
| OP |
| OA |
| OB |
| OP |
| OA |
| OB |
| OP |
| OA |
| OB |
| OA |
| AB |
| OP |
| OA |
| AP |
| AP |
| AB |
解答：
证：（1）
=
+
；
∵A，B，P三点共线
∴
和
共线；
∴存在实数λ使：
=λ
=λ(
-
)；
∴
=
+λ(
-
)=(1-λ)
+λ
；
令x=1-λ，y=λ则：
=x
+y
且x+y=1．
（2）我们来证反过来成立．
x+y=1
∴x=1-y；
∴
=(1-y)
+y
=y(
-
)+
=
+y
；
又
=
+
；
∴
=y
；
根据共线向量基本定理：
和
共线，又
和
有一个公共点A；
∴A，B，P三点共线．
∴反之也成立．
| OP |
| OA |
| AP |
∵A，B，P三点共线
∴
| AP |
| AB |
∴存在实数λ使：
| AP |
| AB |
| OB |
| OA |
∴
| OP |
| OA |
| OB |
| OA |
| OA |
| OB |
令x=1-λ，y=λ则：
| OP |
| OA |
| OB |
（2）我们来证反过来成立．
x+y=1
∴x=1-y；
∴
| OP |
| OA |
| OB |
| OB |
| OA |
| OA |
| OA |
| AB |
又
| OP |
| OA |
| AP |
∴
| AP |
| AB |
根据共线向量基本定理：
| AP |
| AB |
| AP |
| AB |
∴A，B，P三点共线．
∴反之也成立．
点评：本题考查向量的加法运算，共线向量基本定理，向量共线的判定，根据向量的加法运算用其它向量来表示
是证明本题的关键．
| OP |
练习册系列答案
相关题目
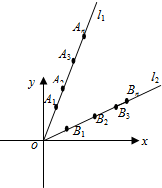已知直线l1：y=3x，l2：y=