题目内容
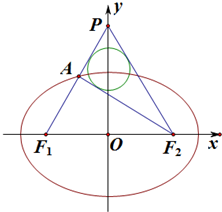
已知椭圆的左、右焦点分别为F1、F2,F1F2=
,P是y轴正半轴上一点,PF1交椭圆于点A,若AF1⊥PF2,且△APF2的内切圆半径为
,则椭圆的离心率是 .
| 10 |
| ||
| 2 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,直角三角形的内切圆半径r=
,结合|F1F2|=
,可得|AF1|2+|AF2|2=10,从而可求|AF1|+|AF2|=3
=2a,即可求得椭圆的离心率.
| ||
| 2 |
| 10 |
| 2 |
解答:
 解:由题意,直角三角形的内切圆半径r=
解:由题意,直角三角形的内切圆半径r=
=
=
=
,
∵|F1F2|=
,
∴|AF1|2+|AF2|2=10,
∴2|AF1||AF2|=8,
∴(|AF1|+|AF2|)2=18,
∴|AF1|+|AF2|=3
=2a,
∵|F1F2|=
,
∴椭圆的离心率是e=
=
=
.
故答案为:
.
 解:由题意,直角三角形的内切圆半径r=
解:由题意,直角三角形的内切圆半径r=| |PA|+|AF2|-|PF2| |
| 2 |
=
| |PA|-|PF1|+|AF2| |
| 2 |
| |AF2|-|AF1| |
| 2 |
| ||
| 2 |
∵|F1F2|=
| 10 |
∴|AF1|2+|AF2|2=10,
∴2|AF1||AF2|=8,
∴(|AF1|+|AF2|)2=18,
∴|AF1|+|AF2|=3
| 2 |
∵|F1F2|=
| 10 |
∴椭圆的离心率是e=
| c |
| a |
| ||
3
|
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查椭圆的几何性质,考查椭圆的定义,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
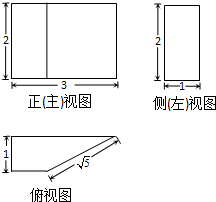
某几何体的三视图如图所示,则该几何体的体积为( )

| A、2 | ||
B、
| ||
| C、4 | ||
| D、5 |
函数h(x)=2sin(2x+
)的图象与函数f(x)的图象关于点(0,1)对称,则函数f(x)可由h(x)经过怎样的变换得到( )
| π |
| 4 |
A、向上平移2个单位,向右平移
| ||
B、向上平移2个单位,向左平移
| ||
C、向下平移2个单位,向右平移
| ||
D、向下平移2个单位,向左平移
|
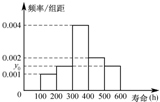 对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如图.
对某电子元件进行寿命追踪调查,所得样本数据的频率分布直方图如图.