题目内容
9.设$a=ln\frac{5}{2},b={log_3}\frac{9}{10},c={π^{0.1}}$,则a,b,c的大小关系是( )| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | b>c>a |
分析 判断三个数与0,1的大小关系,即可推出结果.
解答 解:$0<a=ln\frac{5}{2}<lne=1,b=lo{g}_{3}\frac{9}{10}<0,c={π}^{0.1}>1$
可得c>a>b.
故选:C.
点评 本题考查对数值的大小比较,考查计算能力.

练习册系列答案
相关题目
18.《莱因德纸草书》是世界上最古老的数学著作之一,书中有一道这样的题目:“把100个面包分给5个人,使每个人所得面包数成等差数列,且使最大的三份之和的$\frac{1}{7}$是较小的两份之和,求最小的一份的量.”此题中,若要使得每个人获得的面包数都是整数个,则题中的面包总数“100”可以修改为( )
| A. | 122 | B. | 121 | C. | 120 | D. | 110 |
17.若a=ln2,b=5${\;}^{-\frac{1}{2}}$,c=$\frac{1}{4}$${∫}_{1}^{π}$sinxdx,则a,b,c的大小关系( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | b<c<a |
4.已知集合A={x|2x>$\frac{1}{2}$},B={x|lgx>0},则A∩(∁RB)=( )
| A. | (1,+∞) | B. | (0,1] | C. | (-1,1] | D. | (-1,1) |
14.命题“?x0∈R,x0+1<0或x02-x0>0”的否定形式是( )
| A. | ?x0∈R,x0+1≥0或$x_0^2-{x_0}≤0$ | B. | ?x∈R,x+1≥0或x2-x≤0 | ||
| C. | ?x0∈R,x0+1≥0且$x_0^2-{x_0}≤0$ | D. | ?x∈R,x+1≥0且x2-x≤0 |
19.函数$f(x)=a{log_2}x+a•{4^x}+3$在区间$(\frac{1}{2},1)$上有零点,则实数a的取值范围是( )
| A. | a<-3 | B. | $-\frac{3}{2}<a<-\frac{3}{4}$ | C. | $-3<a<-\frac{3}{4}$ | D. | $-\frac{3}{2}<a<-\frac{1}{2}$ |
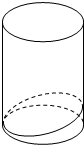 如图,用与圆柱的母线成60°角的平面截圆柱得到的截口曲线是椭圆,则该椭圆的离心率为$\frac{1}{2}$.
如图,用与圆柱的母线成60°角的平面截圆柱得到的截口曲线是椭圆,则该椭圆的离心率为$\frac{1}{2}$.