Question

17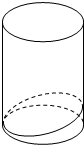．如图，用与圆柱的母线成60°角的平面截圆柱得到的截口曲线是椭圆，则该椭圆的离心率为$\frac{1}{2}$．

Answer 1

分析 由题意可知，椭圆的短轴长等于圆柱的底面直径，由题意结合三角形中的边角关系求得椭圆的长轴长，再由隐含条件求出半焦距，则椭圆的离心率可求．

解答 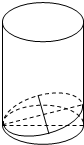解：如图，设圆柱的底面直径为2R，
则椭圆的短轴长2b=2R，b=R．
又截面与圆柱的母线成60°角，
则2a=$\frac{2R}{sin60°}=\frac{2R}{\frac{\sqrt{3}}{2}}=\frac{4\sqrt{3}}{3}R$，
则a=$\frac{2\sqrt{3}}{3}R$．
∴${c}^{2}={a}^{2}-{b}^{2}=\frac{4}{3}{R}^{2}-{R}^{2}=\frac{{R}^{2}}{3}$，
∴$c=\frac{\sqrt{3}}{3}R$．
则椭圆的离心率为e=$\frac{c}{a}=\frac{\frac{\sqrt{3}}{3}R}{\frac{2\sqrt{3}}{3}R}=\frac{1}{2}$．
故答案为：$\frac{1}{2}$．

点评 本题考查平面与圆柱的截线，考查椭圆的性质，考查三角形中的边角关系，是基础题．