题目内容
求下列函数的单调区间:
(1)y=-
sinx;
(2)y=1+
cosx.
(1)y=-
| 1 |
| 3 |
(2)y=1+
| 1 |
| 3 |
考点:正弦函数的单调性,余弦函数的单调性
专题:计算题,三角函数的图像与性质
分析:利用正弦函数、余弦函数的单调性,即可得出结论.
解答:
解:(1)∵y=sinx的单调增区间为[-
+2kπ,
+2kπ],单调减区间为[
+2kπ,
+2kπ](k∈Z),
∴y=-
sinx的单调减区间为[-
+2kπ,
+2kπ],单调增区间为[
+2kπ,
+2kπ](k∈Z);
(2)∵y=cosx的单调增区间为[-π+2kπ,2kπ],单调减区间为[2kπ,π+2kπ](k∈Z),
∴y=1+
cosx的单调增区间为[-π+2kπ,2kπ],单调减区间为[2kπ,π+2kπ](k∈Z).
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
∴y=-
| 1 |
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
(2)∵y=cosx的单调增区间为[-π+2kπ,2kπ],单调减区间为[2kπ,π+2kπ](k∈Z),
∴y=1+
| 1 |
| 3 |
点评:本题考查正弦函数、余弦函数的单调性,考查学生分析理解问题的能力,属于基础题.

练习册系列答案
相关题目
三个数a=60.7,b=0.76,c=log0.76的大小顺序是( )
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、a<c<b |
下列选项中,p是q的必要不充分条件的是( )
| A、p:x=1,q:x2=x |
| B、p:|a|>|b|,g:a2>b2 |
| C、p:x>a2+b2,q:x>2ab |
| D、p:a+c>b+d,q:a>b且c>d |
已知集合A={x|x2-2x-8<0},B={y|y=log2(x2+2)},则A∩B=( )
| A、(-2,-1] |
| B、[-1,4) |
| C、(-∞,4) |
| D、[1,4) |
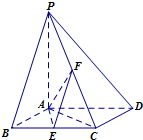 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.